Постановка транспортной задачи в матричной форме. Симплекс метод решения задачи линейного программирования

Петербургский государственный университет путей сообщения

Кафедра «Экономика транспорта»

КУРСОВАЯ РАБОТА

Модели и моделирование на железнодорожном транспорте

	Проверил: Карчик В.Г. Выполнил: Сорова О.В. Шифр: 05-ЭУТц-27

Санкт-Петербург

2009

Содержание:

1.  Постановка транспортной задачи в матричной форме................3стр.

  Решение транспортной задачи методом потенциалов.............4стр.

  Решение транспортной задачи методом разрешающих слагаемых.........................................................................................9стр.

2.  Постановка транспортной задачи в сетевой форме......................17стр.

3.  Задача о назначении..............................................................................23стр.

4.  Симплекс метод решения задачи линейного программирования.....27стр.

1. Постановка базисной задачи в матричной форме.

Транспортная задача – это универсальная постановка задач по распределению ресурсов. Используется в широком диапазоне: от простейших по планированию перевозок одного продукта до сложных производственных транспортных задач по планированию работы отраслевых комплексов в части формирования плана производства и перевозок.

i – номер станции отправления или поставщика,

j – номер станции назначения или потребителя.

Постановка транспортной задачи может быть задана в матричной или сетевой форме. От этого зависит специфика решения:

;

x_ij  - переменная (перевозка из n_i d n_j)

c_ij – критерий оптимальности

a_ij  - ресурс станции отправления

b_ij – потребность на станции назначения

d_ij – ограничение пропускной способности

 

Целевая функция решения задачи:

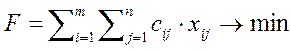                                                        (1)

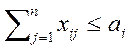,                                                                       (2)

Сумма всех перевозок для каждого поставщика не превышает его ресурсов.

                                                                    (3)

Для каждого потребителя сумма перевозок равна его потребности

                                                                   (4)

                                                                                       (5)

                                                                                        (6)

1.1 Решение транспортной задачи методом потенциалов.

Для решения задач данного типа вначале строится базисный план, удовлетворяющий постановке задачи 2-6, которая затем оптимизируется.

Построенный план называется допустимым.

Рассмотрим построение допустимого плана методом минимальной стоимости.

В таблице матрицы с_ij отыскивается наименьшее значение, куда заносится наибольшее значение перевозки с учетом потребности строки и точности столбца. Затем снова отыскивается наименьшее с_ij и выполняется аналогичная операция.

Допустимый план должен иметь ((m+n)-1) базисных элементов, где m – число строк, n – число столбцов.

Алгоритм решения:

Шаг 1. Расстановка потенциалов выполняется по формуле:

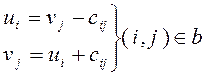
u_i- потенциал строки

v_j – потенциал столбца

Шаг 2. Проверка плана на оптимальность.

Если все небазисные клетки матрицы удовлетворяют условию:

, то план оптимальный, если нет, то переход к Шагу 3.

Шаг 3. Для клетки, в которой найдено максимальное нарушение условия формируется контур перераспределения поставок, который включает в себя данную клетку с нарушением условия  и некоторые из базисных клеток.

В найденном контуре производится метка клеток. Новой клетке, входящей в базис присваивается метка «+», остальные клетки получают метод перемещающейся полярности для строки или столбца. Из клеток помеченных «-» отыскиваем наименьшее значение, оно вычитается из указанных клеток и добавляется к клеткам «+». Значение перевозок в других базисных клетках не меняется. Переход к Шагу 1.

Условия:

Значение критериев оптимальности с_ij

1	7	11	6	9	9
8	3	5	11	6	8
5	4	12	9	8	16
12	8	6	2	5	4
9	10	3	1	12	7

Шаг 1: Построим допустимый (базисный) план.

а1=150	1		7		11		6		9		9
		119				4				20
а2=170	8		3		5		11		6		8
				37		133
а3=120	5		4		12		9		8		16
										120
а4=130	12		8		6		2		5		4
												130
а5=130	9		10		3		1		12		7
						14		116
700/700	b1=119		b2=37		b3=151		b4=116		b5=140		b6=137