|
а1=150 |
1 |
7 |
11 |
6 |
9 |
9 |
||||||
|
119 |
24 |
7 |
||||||||||
|
а2=170 |
8 |
3 |
5 |
11 |
6 |
8 |
||||||
|
23 |
7 |
140 |
||||||||||
|
а3=120 |
5 |
4 |
12 |
9 |
8 |
16 |
||||||
|
14 |
106 |
|||||||||||
|
а4=130 |
12 |
8 |
6 |
2 |
5 |
4 |
||||||
|
130 |
||||||||||||
|
а5=130 |
9 |
10 |
3 |
1 |
12 |
7 |
||||||
|
38 |
92 |
|||||||||||
|
700/700 |
b1=119 |
b2=37 |
b3=151 |
b4=116 |
b5=140 |
b6=137 |
||||||
Найдем целевую функцию F:
F=![]() =
=
=2771
Полученное значение целевой функции совпадает с найденным ранее значением Fметодом потенциалов стр. 6.
2. Сетевая задача в транспортной постановке.
Задача сетевой постановки преимуществом по сравнению с матричной поскольку для отдельных участков указываются ограничения пропускной способности. С другой стороны имеет более громоздкий способ представления информации и поэтому применяется чаще всего с помощью компьютеров.
Алгоритм решения:
Шаг 1. Составляем допустимый план, где n = 1 число потоков (элементов),
n - число узлов, dij – ограничение потока, если xij=dij – такое звено не является базисным.
Шаг 2. Расстановка потенциалов Рi,Рj(только по базисным звеньям)
Шаг 3. Проверка. Получен ли план
оптимальности. Да, если все потенциалы в свободных от потока звеньях ![]() . Если имеется звено, где xij= dij, то для него
. Если имеется звено, где xij= dij, то для него ![]() .
Если условие оптимальности не выполняется, то переход к шагу 4.
.
Если условие оптимальности не выполняется, то переход к шагу 4.
Шаг 4. Из звеньев с нарушением условия оптимальности отыскивается наибольшее нарушение. Это звено становится базисным на следующей итерации, после корректировки базисного плана.
Шаг 5. Корректировка базисного плана.
Сначала для нового звена, которое войдет в базис задачи формируется путь обхода от меньшего потенциала к большему. Далее составляется замкнутый контур обхода, в который включается это звено и некоторые из базисных звеньев. В соответствии с заданными направлениями обхода, отыскиваются противопоточные обходу звенья из них выбирается звено с наименьшими потокам. Величина этого потока присваивается новому базисному звену. Остальные звенья с потоками по контуру корректируются. Если поток на звене совпадает с направлением потока, то к нему добавляется найденное значение потока и вычитается, если направление обхода противоположно потоку.
Переход к шагу 2.
Условие:
Данные по ресурсам поставщиков:
A=90
B=180
C=70
D=80
E=60
Данные по спросу потребителей:
F=43
G=23
H=31
J=19
K=87
L=121
M=67
N=89
Ограничения пропускной способности:
AF=20
CL=20
CD=40
EM=80
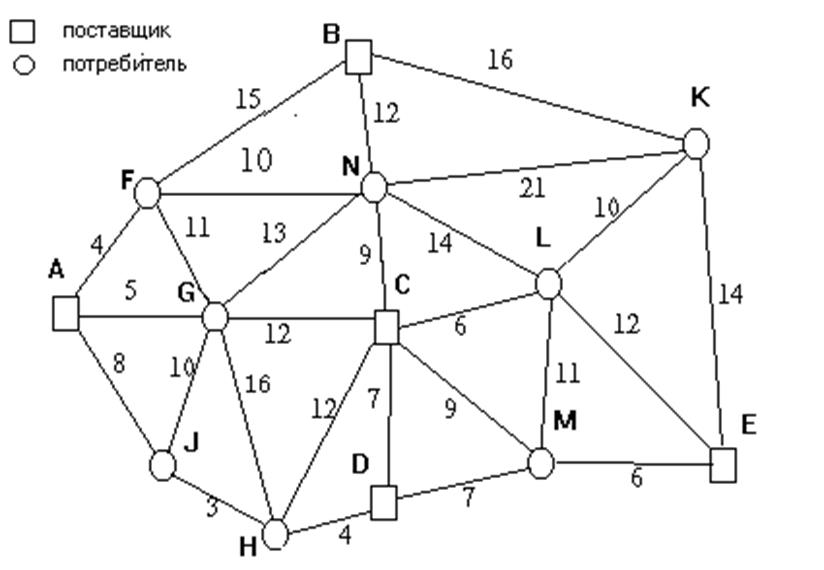
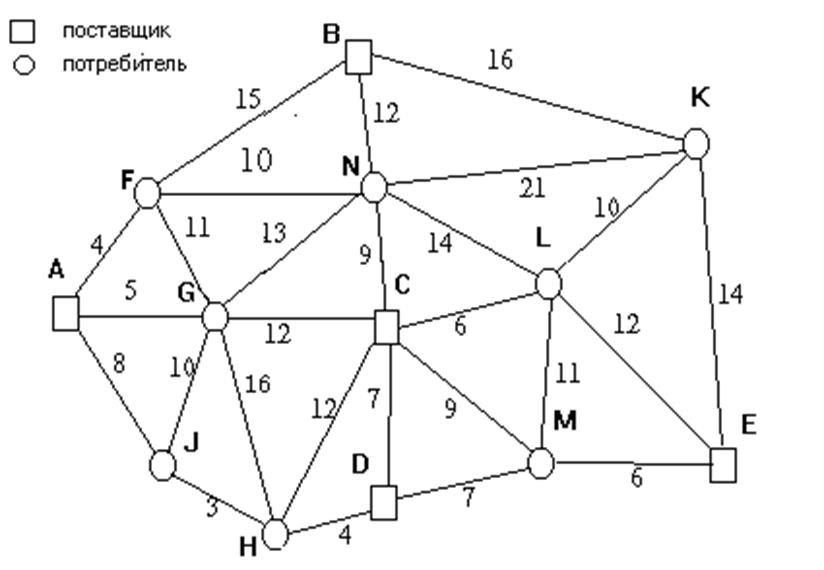
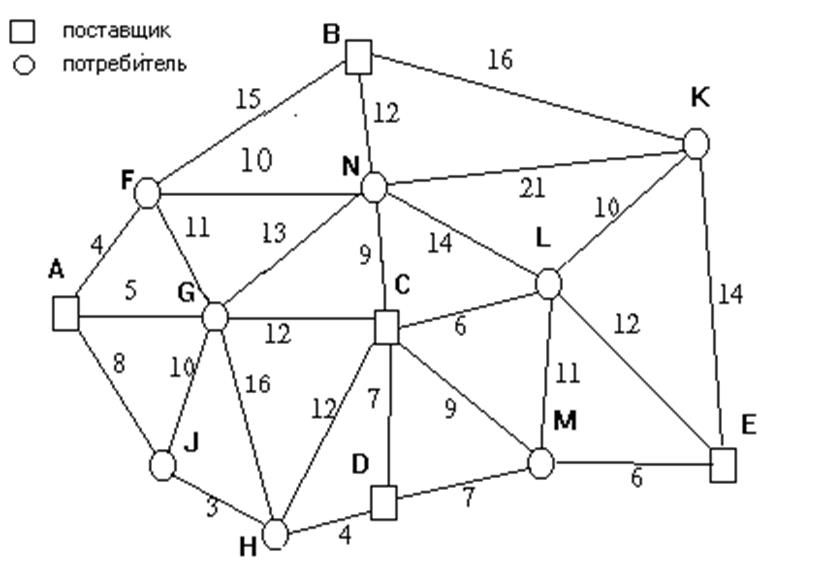
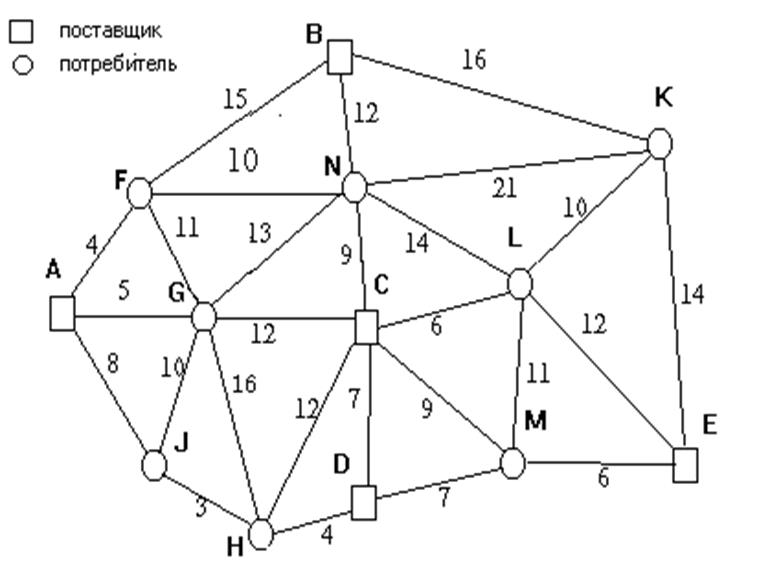
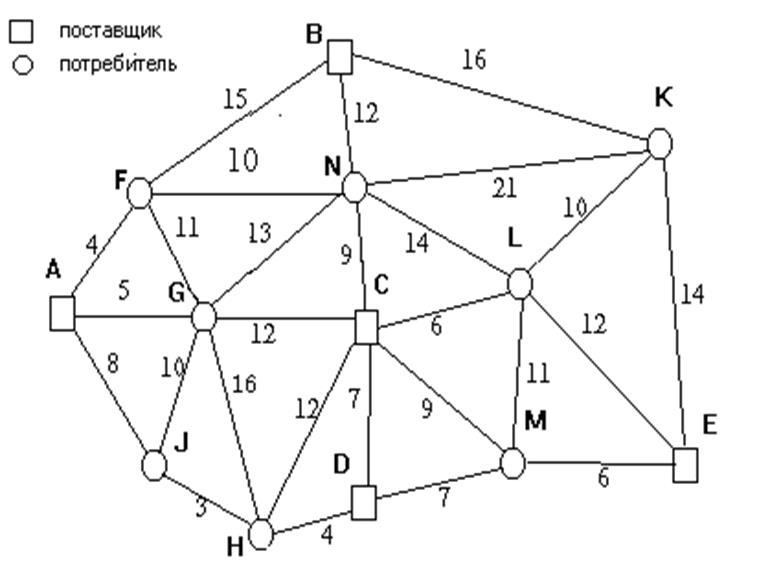
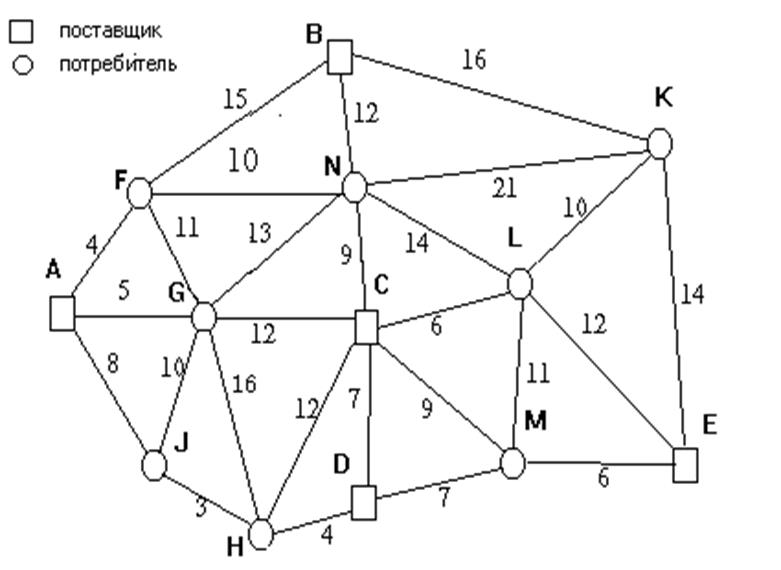


Нарушений нет: план оптимальный.
F=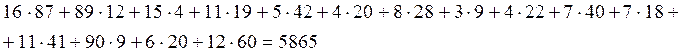
3. Задача о назначении.
Возникает при необходимости оптимизации прикрепления потребителей и поставщиков, где выступают исполнители этих работ.
Эта транспортная задача линейного
программирования в отличии от классической транспортной задачи, где хij принимают целые значения, в данной
задаче 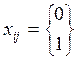
хij – переменная, означающая возможность прикрепления к исполнителю. Если работа прикреплена хij =1, в противном случае хij =0.
Матрица условий этой задачи квадратная (m=n), m-число исполнителей, n-число выполненных «работ» (операций).
Построенный план должен удовлетворять условиям постановки транспортной задачи:
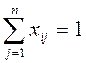 , i=1,2,3…m
(1)
, i=1,2,3…m
(1)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.