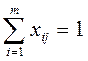Экономика и менеджмент \ Модели и моделирование на транспорте

Постановка транспортной задачи в матричной форме. Симплекс метод решения задачи линейного программирования, страница 10

, j=1,2,3…n                                                                         (2)

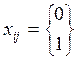                                                                                              (3)

Целевая функция задачи состоит в том, чтобы найти максимальный эффект от деятельности исполнителей:

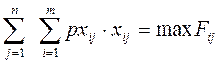
pij-производительность исполнителя i на работе.

Алгоритм решения:

Для решения задачи о назначении используется алгоритм Манкреса, принадлежащий к венгерскому типу.

В таблице приведены исходные данные о производительности четырех машин  A, B, C, D, на четырех работах: N1, N2, N3, N4.

Шаг 1. В каждом столбце матрицы производительности отыскивается  наибольшее значение показателя, из которого вычитаются все остальные.

N1

N2

N3

N4

A

6

5

6

7

B

3

2

4

7

C

7

7

7

7

D

5

4

3

7

N1

N2

N3

N4

A

1

2

1

0

B

4

5

3

0

C

0

0

0

0

D

2

3

4

0

Шаг 2.  В каждой строке матрицы производительности отыскивается  наименьшее значение показателя, из которого вычитаются все остальные.

Шаг 3. Выделение  независимых нулей (элементов  0*) - единственных в строке и столбце одновременно.

Шаг 4. Проверка: получен ли оптимальный план. Да, если количество независимых нулей  равно размерности  матрицы задачи. Нет  -  переход к     шагу 5.

Шаг 5. Метка столбцов.  Каждый столбец, имеющий  0*  закрывается и получает метку "+" вверху.

Шаг 6. Поиск невыделенных нулей.  Если в открытом столбце имеется невыделенный нуль,  он получает метку -  0'. Если строка, содержащая 0' не имеет 0* - переход к шагу 8. Иначе, строка  закрывается справа меткой "+" и открывается столбец, содержащий 0* , и так далее до окончания просмотра всей матрицы и выделения нулей  0'. Переход к  шагу 7.

Шаг 7.  Из совокупности элементов матрицы, состоящих на пересечении открытых столбцов и строк, находится минимальное значение. Эта величина  вычитается из элементов указанной совокупности, и добавляется к элементам, стоящим на пересечении закрытых столбцов и строк. Значения остальных элементов матрицы сохраняются. Все метки строк, столбцов, 0', 0*  переносятся из предыдущей таблицы в данную,  переход к шагу 6.

Шаг 8.  Формирование цепочки типа:  0'- 0*- 0'- 0*...0' . Все элементы 0' данной цепочки заменяются на элементы вида 0*, Все элементы 0'* данной цепочки снимаются. Также убираются все метки строк и столбцов  и метки 0'. Переход к шагу  4.

№1 шаг 3,4,5,6,7                                           №3 шаг 5,6,7 

N1

N2

N3

N4

A

1

2

3

0*

B

4

5

3

0

C

0*

0'

0

0

D

2

3

4

0

N1

N2

N3

N4

A

0*

1

0'

0

B

3

4

2

0*

C

0

0*

0'

1

D

1

2

3

0

№2 шаг6,8,4                                                          №4 шаг 6,8

N1

N2

N3

N4

A

0'

1

0

0*

B

3

4

2

0'

C

0*

0'

0

1

D

1

2

3

0

N1

N2

N3

N4

A

0*

1

0'

1

B

3

4

2

0

C

0

0*

0'

2

D

0'

1

2

0

№5 шаг 4. получен оптимальный план.

Скачать файл