




















ЛЕКЦИЯ 47
Смешение и транспортировка сыпучих материалов
47.1. Общие сведения
Процесс перемешивания зернистых (сыпучих) материалов широко применяют в различных отраслях промышленности, например, в производстве строительных материалов, при составлении шихты в коксохимии и металлургической промышленности, приготовлении красителей, лекарственных препаратов, и т. д. В некоторых процессах необходимо перемешивать грубодисперсные суспензии при большой доле твердой фазы (бетонные смеси, строительные растворы, керамические массы).
Смешение сыпучих материалов является специфическим случаем перемешивания, что обусловлено особым характером систем, состоящих из твердых частиц. В динамике такие системы ведут себя иначе, чем при перемешивании в жидких средах и поэтому требуют отдельного рассмотрения.
При смешении зернистых материалов основной задачей, как правило, является уменьшение композиционной неоднородности смеси, так как механические, физические и химические свойства, а также внешний вид изделий существенно зависят от этого параметра. Однако строгую количественную взаимосвязь между параметрами системы, способом перемешивания и его эффективностью до настоящего времени установить не удалось. Даже для бинарной системы, уравнения для оценки степени перемешивания очень сложно и требует знания многих факторов, которые трудно определить на практике.
Для оценки эффективности смесителя определяющим фактором является распределение частиц, которое достигается после определенной продолжительности гомогенизации. Мерой оценки интенсивности работы смесителя может быть или стандартное отклонение состава пробы, отобранной по истечении некоторого времени гомогенизации, или отношение действительного отклонения случайной смеси к стандартному теоретическому отклонению идеально перемешанной смеси. Второй показатель имеет то преимущество, что по мере повышения качества смешения он приближается к единице и более наглядно определяет качество смешения.
47.2. Отклонение весовой частоты пробы
Рассмотрим бинарную смесь компонентов P и Q с весовой долей каждого компонента GP и GQ. Состав такой смеси определяется уравнениями:
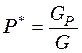 и
и 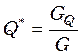 , (47.1)
, (47.1)
где
![]() – концентрации отдельных компонентов
смеси в долях единицы, следовательно,
– концентрации отдельных компонентов
смеси в долях единицы, следовательно, ![]() ,
, ![]() – общее количество смеси.
– общее количество смеси.
Для оценки работы смесителя из общей смеси отбирают пробу небольшого
объема весом ![]() . Необходимым условием является отсутствие
влияния отбора пробы на общий состав и количество смеси, т. е.
. Необходимым условием является отсутствие
влияния отбора пробы на общий состав и количество смеси, т. е. ![]() .
.
Это небольшое весовое количество также состоит из двух компонентов ![]() . Взаимное отношение обоих весовых
количеств будет различным для каждой пробы.
. Взаимное отношение обоих весовых
количеств будет различным для каждой пробы.
Общий вес пробы:
![]() . (47.2)
. (47.2)
Общее количество смеси равно сумме всех этих малых весовых долей:
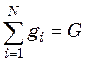 . (47.3)
. (47.3)
Концентрации каждого компонента выражают в долях единицы в любой пробе и
обозначают ![]() для компонента
для компонента ![]() и
и ![]() для компонента
для компонента ![]() . Следовательно:
. Следовательно:
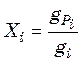 ;
; 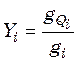 ; (47.4)
; (47.4)
![]() . (47.5)
. (47.5)
В идеальной смеси сумма всех весовых долей всех проб даст соответствующее весовое количество компонентов в общей смеси:
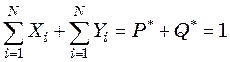 . (47.6)
. (47.6)
В случайной смеси значения ![]() всегда отличаются от
значений, требуемых заданной степенью перемешивания и данных
всегда отличаются от
значений, требуемых заданной степенью перемешивания и данных ![]() . В соответствии с теорией ошибок можно
установить рассеяние весовых частот
. В соответствии с теорией ошибок можно
установить рассеяние весовых частот ![]() по сравнению с
требуемыми значениями
по сравнению с
требуемыми значениями ![]() по формулам:
по формулам:
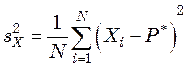 ; (47.7)
; (47.7)
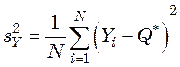 , (47.8)
, (47.8)
где
![]() – рассеяние весовых частот от требуемого
значения.
– рассеяние весовых частот от требуемого
значения.
В двух последних уравнениях выражения в скобках идентичны, поэтому можно записать общее уравнение отклонения весовых частот в пробе для бинарной смеси:
![]()
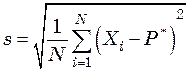 . (47.9)
. (47.9)
Уравнение (24.9) определяет отклонение произвольной смеси. Отклонение
весовых частот идеальной смеси обозначим ![]() , тогда
степень смешения определяется уравнением
, тогда
степень смешения определяется уравнением
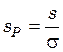 . (47.10)
. (47.10)
Чем ближе качество смеси к идеалу, тем ближе величина ![]() к единице.
к единице.
На величину отклонения ![]() , кроме переменных,
входящих в уравнение (24.9), оказывают влияние отношение веса частиц, их распределение
в смеси и величина отобранной пробы.
, кроме переменных,
входящих в уравнение (24.9), оказывают влияние отношение веса частиц, их распределение
в смеси и величина отобранной пробы.
Для получения зависимости отклонения частоты распределения частиц ![]() в уравнение (24.9) вместо переменной
весовой концентрации
в уравнение (24.9) вместо переменной
весовой концентрации ![]() подставим ее значение,
выраженное через частоту
подставим ее значение,
выраженное через частоту ![]() ,
,
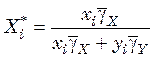 , (47.11)
, (47.11)
где
![]() – средний вес частиц смеси.
– средний вес частиц смеси.
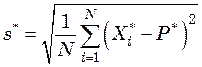 . (47.12)
. (47.12)
Для многокомпонентных смесей расчетные уравнения очень сложны и ознакомиться с ними можно в специальной литературе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.