Смешение и транспортировка сыпучих материалов, страница 2

Кроме изложенного выше применяют еще несколько статистических  методов оценки (количественных и качественных), имеющих применение для оценки качества зернистой смеси. Наиболее часто для этого используют распределение Стьюдента (фактор ), распределение Фишера (фактор ) и фактор  (хи-квадрат).

Распределение Стьюдента позволяет оценить полноту смешения двух зернистых компонентов смеси по формуле

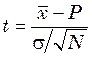                                                  ,                                               (47.13)

где  – параметр распределения Стьюдента;  – среднее арифметическое значение концентрации для всех проб;  – действительная концентрация компонента во всей системе;  – стандартное отклонение системы, определяемое по уравнению

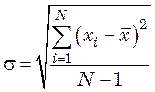                                           ,                                        (47.14)

 – число проб;  – концентрация  пробы.

Практически установлено, что при оценке качества зернистых смесей удовлетворительным является уровень доверительности 0,95. В связи с этим из таблиц величины , которые приводятся в литературе по математической статистике, определяется, может ли при числе степеней свободы  полученное значение  случайно встретиться чаще, чем один раз на двадцать (т. е. меньше ли значение , чем приведенное в таблице для числа степеней свободы  и уровня допуска 0,05).

Распределение Фишера применяют при увеличении масштаба смесителя. Если в лабораторных условиях при степени смешения, которая считается удовлетворительной, для  проб найдена дисперсия состава проб , а для смеси, полученной в промышленном аппарате, для  проб найдена дисперсия состава , то фактор  дает возможность оценить на данном уровне доверительности, является ли степень смешения, достигнутая в промышленном аппарате, тоже удовлетворительной. Когда , тогда статистический фактор не нужен, так как степень смешения в промышленном смесителе выше, чем в лабораторном смесителе. Если , необходимо определить отношение

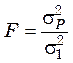                                                    .                                                 (47.15)

Затем из таблиц величины  определяют, может ли при числах степеней свободы числителя и знаменателя, соответственно равных , такое большое значение  случайно встретиться чаще, чем один раз на двадцать (т. е. меньше ли значение , чем приведенное в таблице для уровня допуска 0,05 и чисел степеней свободы ). Если значение  меньше, чем приведенное в таблице, то можно заключить с 5 %-й вероятностью совершения ошибки, что смесь, полученная в промышленном смесителе, имеет удовлетворительную степень смешения.

Распределение частоты состава проб (фактор ) используют при достаточно большом числе проб, отобранных из зернистой смеси. На основании результатов анализа проб строят график (рис.47.1), на оси абсцисс которого откладывают состав (долю данного компонента в пробе), а на оси ординат – частоту его появления (число проб с данным составом). Такой график называется распределением частоты состава проб и хорошо иллюстрирует состояние смешения. Неупорядоченная смесь характеризуется нормальным распределением, а фактор  позволяет оценить, является ли распределение нормальным.

Если – множество частот появления данных составов проб, а – множество соответственно ожидаемых частот, рассчитанных для данных составов по нормальному распределению, то величину определяют по уравнению

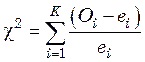                                            ,                                         (47.16)

где  – число пар замеченных и ожидаемых частот, которые сравниваются друг с другом (число проб должно быть подобрано так, чтобы на принятом уровне доверительности 0,95 ожидаемая частота всегда была больше или равна пяти).