Уравнения состояния газов воздуха и термодинамика атмосферы

 13. Уравнения состояния газов воздуха и термодинамика атмосферы

13.1. Уравнение состояния

Уравнение состояния идеального газа (Клапейрона-Менделеева)[1]:

                                                    p = nkT.                                                                    (13.1)

Здесь p – давление газа, T – абсолютная температура, n – концентрация (число атомов или молекул газа в единице объема), k – постоянная Больцмана. Коррекция и переход к более точному уравнению Ван-Дер-Ваальса не нужны, поскольку давление и температура в атмосфере обычно таковы, что поправки не играют заметной роли.

В случае смеси газов парциальное давление каждого подчиняется уравнению: p_i = n_ikT, где p_i – парциальное давление (давление данного газа, когда остальные газы смеси удалены); n_i – концентрация газа с номером i (полное давление в смеси газов определяется суммой парциальных давлений: .

Умножим уравнение состояния (13.1) на V=N/n, где N – число Авогадро (число молекул в одном моле газа); тогда V – объем 1 моля при тех же условиях (давлении и температуре). Тогда

                                                  pV = RT,

где R = Nk – универсальная газовая постоянная.

Введем υ=V/μ – объем единицы массы газа. Здесь μ – масса одного моля газа (молекулярный вес). Тогда уравнение состояния принимает вид

                                                pυ=RT / μ.

Если теперь обозначить  1/υ=ρ – плотность газа (масса в единице объема), получим

                                                       p=RTρ/μ.

Для смеси газов имеем

                                           p=∑p_i=RT ∑(ρ_i/μ_i)=RTρ_в/μ_в ,                                                   (13.2)

где ρ_в=∑ρ_i  - суммарная плотность смеси. Средний молекулярный вес определяется согласно  формуле

                                       ,

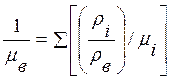чтобы выполнялось последнее равенство в (13.2). Поскольку состав воздуха до высот около 100 км не практически не меняется, можно записать p=ρ_вR_вT, где

                   R_в=R/μ_в=287.05 Дж/(кг·К),  μ_в=28.964,  μ_О2=32,  μ_N2=28.

Из уравнения состояния ρ_в=1/υ=р/(R_вТ)  при р=р_о , Т=20 ^оС  имеем    r_в=1.3 кг/м³.

Влажный воздух

В  случае присутствия влаги к воздуху добавляется водяной пар, и полное давление получается равным

                                               р=р_в+р_пара=р_в+е.

Здесь p_в -  парциальное давление сухого воздуха,  e -  стандартное обозначение парциального давления водяного пара. μ_пара ≈ 18, R_пара=461.5 Дж/(кгּК). В результате имеем

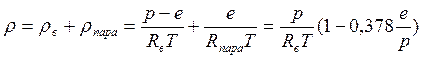 или .

Иногда вводят виртуальную температуру: Т_v=Т(1+0,378 е/р). Тогда для этой температуры выполняется привычное уравнение состояния для сухого воздуха[2]:

                                                      .

Возможно, для метеорологии такой «хитрый прием» и имеет некоторый смысл для упрощения практических расчетов, но для физики атмосферы это просто лишний параметр.

Барометрическая формула

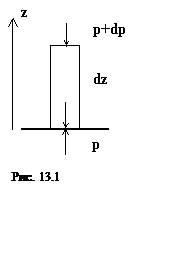
Барометрическая формула определяет зависимость давления воздуха от высоты над поверхностью Земли. Мы предполагаем, что воздух покоится (отсутствуют вертикальные ускорения)[3]. Тогда сумма действующих на выделенный объем сил (вертикальной составляющей силы давления и силы тяжести) должна равняться нулю. Отсюда получаем (см. рис. 13.1)

dp= -ρgdz      

или

                              ,

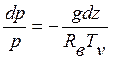где мы воспользовались уравнением состояния. Величину H(Т_ν)=R_вT_ν/g ≈ 8 км   для Т=0^оС называют высотой однородной атмосферы. Это толщина атмосферы, если весь воздух в ней привести к нормальному давлению при температуре  T_ν. После интегрирования получаем

                                              .

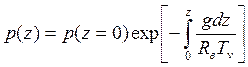Здесь g (ускорение свободного падения) зависит от высоты и широты, однако в большинстве случаев такой зависимостью можно пренебречь).  Зато почти всегда следует учитывать зависимость виртуальной температуры от высоты: T_ν=T_ν (z).

Для не очень толстого слоя со средней температурой Т₀:

                                                ,

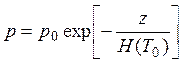где  p₀- давление у поверхности Земли. Здесь следует обратить внимание на то, что показатель экспоненты обратно пропорционален температуре слоя. Следовательно, в более теплом воздухе давление убывает с высотой медленнее, чем в более в холодном. Иными словами, если рядом соседствуют теплая и холодная воздушные массы (с одинаковым давлением у поверхности Земли), на высоте давление в теплой воздушной массе будет больше, чем в холодной. Градиент давления приводит к возникновению силы и является причиной горизонтального перемещения воздуха из области с более высоким давлением в область с более низким давлением. Именно таким образом разница в степени нагрева вызывает движение воздуха.

13.2. Первое начало термодинамики

Первое начало термодинамики утверждает, что количество тепла dQ, сообщенное изолированной системе, расходуется на приращение внутренней энергии dU и на совершение работы против внешних сил dA:

.

Внутренняя энергия единицы массы идеального газа равна с_vT и представляет собой кинетическую энергию движения составляющих его атомов и молекул ( ½kT на каждую степень свободы каждой частицы)[4]. Множитель с_v – теплоемкость газа при постоянном объеме.