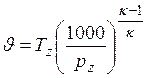Уравнения состояния газов воздуха и термодинамика атмосферы, страница 4

                                       ,

где , а давление измерено в миллибарах. С учетом приближенной величины сухоадиабатического градиента можно записать     

                                                    ,

где высота измерена в метрах. Это та температура, которую будет иметь воздух, если его привести адиабатически к нормальному давлению. Очевидно, что при адиабатических процессах потенциальная температура не меняется, в то время как обычная температура может меняться значительно. Если немножко поманипулировать формулами, то легко получить:

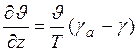    .         (13.2)

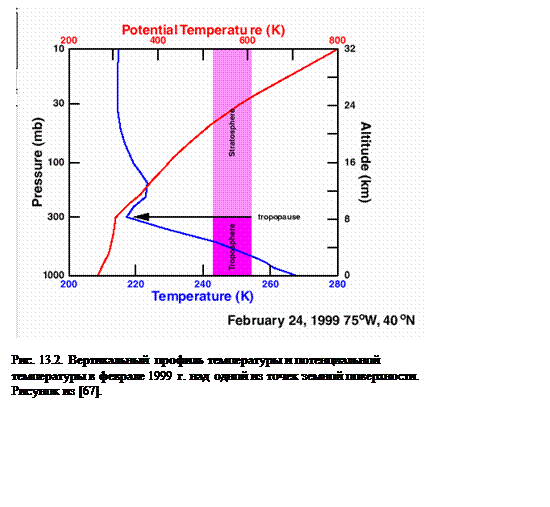
Для средних условий геометрический градиент γ близок к величине 0.6°/100 ми меньше γ_a. Следовательно, обычно в атмосфере потенциальная температура растет с высотой. В стратосфере температура воздуха медленно повышается, значит, потенциальная температура растет с высотой намного быстрее, чем в тропосфере. Пример показан на рис. 13.2.

Чтобы получить приведенную выше формулу, прологарифмируем выражение для потенциальной температуры:

                                    .

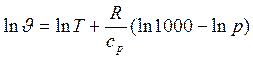Дифференцируя по высоте и используя уравнение состояния и барометрическую формулу, получаем:

             ,

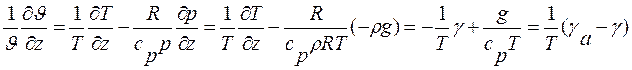откуда и следует формула для геометрической производной от потенциальной температуры по высоте.

Используя равенство  и приведенные выше соотношения, легко установить связь между изменением энтропии и изменением потенциальной температуры:

                                           ,

откуда просматривается также и связь потенциальной температуры со статистическим весом состояния. Попросту  говоря,  рост потенциальной температуры означает рост энтропии и рост статистического веса.

Влажноадиабатический градиент температуры

До тех пор, пока не наступило состояние насыщения водяного пара в воздухе, он может рассматриваться, как малая газовая составляющая, слабо влияющая на термодинамическое состояние воздуха. Таким образом, приведенные выше уравнения применимы также и к влажному ненасыщенному воздуху. Хотя теплоемкость пара больше, чем у сухого воздуха, содержание его невелико, и связанными с этим изменениями пренебрегают. Следует только подчеркнуть, что по мере снижения температуры воздуха относительная влажность увеличивается. Оценки показывают, что для адиабатически поднимающегося влажного воздуха (то есть, при градиенте ~1⁰/100 м) относительная влажность увеличивается приблизительно на 6% на каждые 100 м поднятия. Эта оценка справедлива, по крайней мере, для нижнего километра средних широт [17].

Ситуация резко меняется, когда воздух достигает состояния насыщения. В случае насыщенного воздуха на присутствующих всегда в атмосфере  инородных частицах (центрах конденсации) при расширении и охлаждении начинается конденсация пара, зарождаются капли воды и  происходит выделение скрытой теплоты конденсации. Это замедляет дальнейшее охлаждение воздуха. Теплота конденсации равна теплоте испарения и составляет приблизительно  5 теплот нагрева воды до точки кипения от 0 ⁰С при нормальном давлении.

Наличие в атмосфере большого числа центров конденсации препятствует в общем случае возникновению значительного перенасыщения. Обычно оно не превышает 1-2%. В то же время число частиц, могущих служить ядрами сублимации (льдообразования) не столь велико. Поэтому при отрицательных температурах возможны значительные перенасыщения относительно льда.

Кстати, коль скоро заговорили о характеристиках влажного воздуха, назовем их все:

         Упругость (парциальное давление) водяного пара: e.

Абсолютная влажность (плотность пара): .

Относительная влажность: , где Е – парциальное давление насыщенного пара над плоской поверхностью чистой воды (при тех же температурных условиях!).

Дефицит влажности: d = Е–е (от него зависит скорость испарения).

Отношение смеси: отношение массы водяного пара к массе  сухого воздуха в этом же объеме: