Уравнения состояния газов воздуха и термодинамика атмосферы, страница 2

Легко убедиться, что работа, совершаемая при расширении при постоянном давлении равна:           

                                       .

Здесь  F - сила давления,  действующая на элемент поверхности dS, dx - перемещение поверхности. Следовательно dQ= с_vdT+pdV. Используя уравнение состояния pυ=RT  (υ – удельный объем), можно получить

dQ= (с_v+R)dT-υdp=c_pdT- υdp, 

так как с_v+R=c_p, или      

                                           dQ= c_pdT - RT dp/p.

Здесь c_p, согласно термодинамике, обозначает теплоемкость при постоянном давлении.

Если изменение состояния газа происходит без обмена теплом с внешней средой, процесс называется адиабатическим. Тогда из предыдущего соотношения получаем

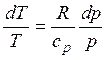
или lnT = R / c_p ln p + const. Отсюда

                                               ,

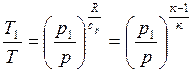где к=с_p/c_v=(c_v+R)/c_v – показатель адиабаты. Если подставить Т из уравнения состояния,  получим pυ^к = const. Показатель адиабаты для сухого воздуха[5] к =1.40, (к -1)/ к =0.288.

Изотермический процесс  характеризуется постоянством температуры (теплообмен с «резервуаром» настолько эффективен, что температура все время совпадает с температурой «резервуара»): T=const. Тогда из уравнения состояния воздуха получаем pυ = const.

Атмосферные процессы, строго говоря, не являются ни адиабатическими, ни изотермическими, а имеют некоторый промежуточный характер. При движении масс воздуха в той или иной степени происходит теплообмен между ними и окружающей средой. Возможно также нагревание и остывание за счет поглощения и испускания излучения. Все это нарушает условия адиабатичности. Для таких реальных процессов в некоторых случаях справедлива та же формула

pυ ^к = const,

но  имеет промежуточные значения между 1.40 и 1. Такие процессы называются политропными, а параметр  называют показателем политропы[6].

Тем не менее,  часто влияние источников тепла и обмен теплом с окружающей средой в атмосфере малы по сравнению с изменением внутренней энергии газа. В таких случаях процессы можно приближенно рассматривать как адиабатические на достаточно коротких временных интервалах, пока не начинают заметно сказываться эффекты обмена теплом.

13.3. Энтропия и второе начало термодинамики

            В термодинамике понятие «энтропия» было введено немецким физиком Р. Клаузиусом[7] (1865). Он показал, что процесс превращения теплоты в работу подчиняется второму началу термодинамики, которое математически формулируется с использованием понятия энтропии как функции состояния  среды (в нашем случае – воздуха). В соответствии со сказанным, изменение состояния порождает в общем случае изменение энтропии, а одному и тому же состоянию соответствует одна и та же энтропия, независимо от способа достижения данного состояния. Согласно второму началу термодинамики, изменение энтропии системы связано с теплом , сообщаемым системе, соотношением

                                                                 .

Поскольку энтропия является функцией состояния, разность энтропий двух различных состояний системы не зависит от способа, каким осуществлен перевод системы  из одного состояния в другое.

Статистическая физика связывает понятие энтропии с вероятностью осуществления данного макроскопического состояния системы (Л. Больцман[8], 1872). Здесь речь идет  именно о макроскопическом состоянии, которое характеризуется значениями термодинамических характеристик, а не значениями характеристик всех атомов и молекул, составляющих систему. В свою очередь, совокупность характеристик всех атомов и молекул определяет  микроскопическое состояние системы. Если предположить, что все микроскопические состояния равновероятны[9], то согласно теореме о сложении вероятностей, упомянутая  выше вероятность реализации данного макроскопического состояния пропорциональна числу различных микроскопических состояний, которые на макроскопическом уровне соответствуют рассматриваемому макроскопическому состоянию.