Уравнения состояния газов воздуха и термодинамика атмосферы, страница 3

Согласно такой трактовке, система всегда стремится перейти из менее вероятного состояния в более вероятное, что соответствует увеличению энтропии. Просто это означает, что наиболее вероятному макроскопическому состоянию системы соответствует то, которому  можно сопоставить наибольшее число микроскопических состояний. С позиций термодинамики возможны только такие термодинамические процессы, в ходе которых энтропия либо остается постоянной (адиабатический процесс, ), либо увеличивается.

Число микроскопических состояний системы, отвечающих заданному макроскопическому состоянию называется статистическим весом состояния. Система, предоставленная сама себе, очевидно, стремится перейти в состояние с максимально возможным статистическим весом. В статистической физике показывается, что энтропия однозначно определяется величиной статистического веса системы z посредством соотношения

                                              ,

где  k- постоянная Больцмана. Из соотношения сразу видно, что энтропия системы, состоящей из двух частей, есть сумма энтропий частей, поскольку, очевидно, статистический вес полной составной системы есть произведение статистических весов ее частей согласно определению статистического веса.

Закон, определяющий направление тепловых процессов, эквивалентен закону возрастания энтропии: при всех происходящих в замкнутой системе тепловых процессах энтропия системы возрастает (или, по крайней мере, остается постоянной). Максимально возможное значение энтропии замкнутой системы достигается в состоянии теплового (термодинамического) равновесия. Это утверждение является более точной формулировкой второго начала термодинамики.

13.4. Градиент температуры

Сухоадиабатический градиент температуры

Введем понятие частицы воздуха, означающее наибольший при заданных внешних условиях и условиях движения объем воздуха, в пределах которого физические характеристики, способные повлиять на изучаемый процесс, одинаковы. Ясно, что понятие частицы весьма субъективно, главное, чтобы частица была однородна по своим характеристикам и перемещалась как целое в процессе исследуемого движения. На самом деле такая частица, несмотря на малые размеры, является частицей среды, и к ней применимы все законы, относящиеся к сплошной среде[10]. 

Давайте в приближении адиабатичности процесса найдем изменение температуры частицы воздуха при перемещении на другую высоту. Пусть на высоте z она имела давление и температуру p, T, а на уровне z+dz  соответственноp+dp, T+dT.

Из первого начала термодинамики с учетом адиабатичности процесса имеем 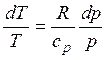. Очевидно, что во всех случаях (даже при относительно большой скорости перемещения, но значительно меньшей скорости звука) давление в частице быстро сравнивается с давлением окружающего воздуха (это - так называемое квазистатическое условие). Падение давления при увеличении высоты в условиях отсутствия движения атмосферы равно весу столба воздуха толщиной dz:

                             ,                                                           (13.1)

где ρ₀ – плотность окружающего воздуха, T₀ – температура окружающего воздуха. Тогда

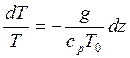                                   или .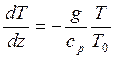

В реальных ситуациях отношение  очень близко  к единице. Поэтому принимается, что

                                                      .

Величина называется сухоадиабатическим градиентом[11]. Если подставить значения постоянных, получим  γ_a≈1°/100 м. Адиабатический градиент смещающейся по высоте частицы воздуха называют также индивидуальным градиентом. Его следует отличать от вертикального градиента температуры в окружающем частицу воздухе, , который называется геометрическим или локальным и обозначается 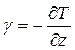. В атмосфере встречаются самые разнообразные значения γ, как бóльшие, так и меньшие адиабатического градиента γ_a..

Теперь мы можем ввести понятие потенциальной температуры: