Уравнения состояния газов воздуха и термодинамика атмосферы, страница 6

13.5. Условия вертикальной устойчивости сухого воздуха

Состояние атмосферы (или стратификация), при котором небольшие вертикальные движения в атмосфере развиваются далее, захватывая следующие слои воздуха, называется неустойчивым.

Наоборот, если начавшиеся вертикальные движения не развиваются, а затухают, говорят об устойчивой стратификации. Получить количественные критерии устойчивости стратификации атмосферы можно, используя метод частицы.

Метод частицы. Для оценки устойчивости атмосферы судят о перемещении отдельной воздушной частицы. Пусть имеется частица объема V и  температуры Т' на высоте z, где воздух имеет давление p и температуру T. Мы считаем, что частица перемещается достаточно медленно, чтобы давление в ней совпадало с давлением окружающей среды. Тогда на нее действует выталкивающая сила f = Vg (r-r'), где r' – плотность воздуха в частице. Относя силу к единице массы, находим ускорение:

                                           ,

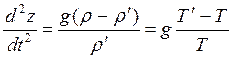где мы воспользовались соотношением  , которое следует из уравнения состояния и условия равенства давлений в частице и окружающей среде. Из этого равенства следует ,  и правая часть вышеприведенного равенства.

Предполагая адиабатичность процесса перемещения[14], найдем высоту , на которой произойдет выравнивание температур, и движение  прекратится (вернее, обратится в нуль ускорение). Для небольших интервалов изменения высоты температуру окружающего воздуха можно определить с использованием геометрического градиента температуры. Изменение температуры адиабатически поднимающейся частицы определяется адиабатическим градиентом:

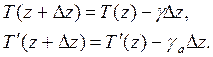
Приравнивая левые части, находим искомую высоту, на которой температура частицы сравнивается с температурой окружающего воздуха:

                                          .

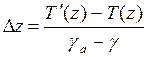Таким образом, высота подъема зависит от начальной разности температур  и величины вертикального градиента температуры  g в окружающем воздухе.

Так, для DТ = 2⁰ (перегрев) при инверсии (g = -1,5⁰/100 м) получаем  Dz = 75 м;

                                              при изотермии (g = 0) -                               Dz = 200 м;

                                              при среднем градиенте (g = 0,6⁰/100 м) -  Dz = 500 м.

Если g = g_а – движение формально не прекращается.

Если g > g_а – движение происходит вниз.

Эти оценки сделаны в предположении, что перемещение воздушной частицы происходит адиабатически. На самом деле всегда имеет место некоторый теплообмен с окружающей средой. Однако качественная картина сохраняется.

Вертикальные движения более интенсивны при больших градиентах g и быстро затухают в слоях изотермии и инверсии.

Предположим, что разность DТ = 0, однако частица получила некоторый импульс в вертикальном направлении. Тогда при g < g_а, поднявшись, частица окажется холоднее окружающего воздуха и будет вынуждена опуститься[15]. Очевидно, такое состояние атмосферы является устойчивым. При g > g_а воздушная частица будет становиться все теплее и будет продолжать свое движение. Это говорит о неустойчивом состоянии атмосферы. При g = g_а – состояние атмосферы – безразличное, поскольку разность температур не меняется с высотой[16].

При безразличном состоянии атмосферы потенциальная температура воздуха не меняется с высотой, как это следует из формулы для градиента потенциальной температуры, приведенной ранее. При устойчивом состоянии потенциальная температура растет с высотой, при неустойчивом – падает[17].

Из проведенного обсуждения видно, что устойчивость атмосферы количественно определяется разностью адиабатического и геометрического градиентов температуры. Поэтому величину  называют параметром статической устойчивости[18]. Действительно, чем больше величина s, тем устойчивее атмосфера. Когда же параметр устойчивости снижается до нуля или становится отрицательным, вместе с ним понижается и устойчивость атмосферы.