Уравнения состояния газов воздуха и термодинамика атмосферы, страница 7

Что будет в случае влажного воздуха? Для ненасыщенного влажного воздуха условия вертикального равновесия почти такие же. В случае, когда возможна конденсация, справедлива следующая схема:

g > g_а и тем более > g_ва – неустойчивое состояние атмосферы;

g = g_а, но g > g_ва – сухобезразличное, но влажнонеустойчивое состояние;

g < g_а, но g > g _ва – сухоустойчивое, но влажнонеустойчивое состояние;

g < g_а, но g = g _ва – сухоустойчивое, но влажнобезразличное состояние;

g < g_а, и   g < g _ва – устойчивое состояние.

Метод слоя. Оценки устойчивости атмосферы, приведенные выше, получены с использованием так называемого «метода частицы». В рамках данного метода предполагается, что изолированная частица воздуха движется в неподвижной среде. Однако на самом деле это не так. Очевидно, что перемещение отдельных частиц вверх должно вызывать компенсационное нисходящее движение окружающего воздуха. Учет этого обстоятельства осуществляется в рамках «метода слоя». Идея метода заключается в следующем.

Пусть в вертикальном столбе сечением S_­  происходит восходящее движение воздуха, а в окружающем этот столб цилиндре с сечением в виде кольца площадью S_¯ происходит опускание воздуха. Считается, что перемещение воздуха происходит адиабатически, горизонтальные движения отсутствуют, и суммарный перенос массы через любой горизонтальный уровень отсутствует.       Названных условий достаточно для получения критерия вертикальной устойчивости атмосферы: условия, когда восходящий поток не ускоряется, а замедляет свое движение.

Анализ показывает, что получаемые критерии, совпадают с найденными ранее по методу частицы в случаях, когда восходящие и нисходящие потоки одновременно не насыщены или насыщены влагой (помимо пара в воздухе присутствуют капли воды) [3]. Новый результат получается, когда восходящий поток насыщен влагой, а нисходящий – не насыщен. В этом случае возможна условно устойчивая стратификация атмосферы, когда устойчивость не имеет места для частиц малого размера, но имеет место для частиц большого размера. Эти «тонкости» теории оказываются важными при рассмотрении процессов образования и развития кучевых облаков.

Сверхадиабатические градиенты температуры

Давайте установим связь между вертикальным градиентом плотности воздуха и градиентом температуры. Логарифмируя и дифференцируя уравнение состояния воздуха, получаем

                         .

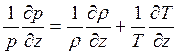Отсюда с учетом

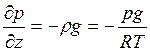
находим

                       .

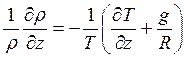Зная вертикальное распределение температуры, с помощью этой формулы можно определить, как меняется плотность с высотой. Но нам сейчас интересно узнать, при каком градиенте температуры плотность воздуха неизменна: ? Из приведенной выше формулы получаем

                                .

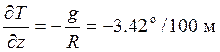Получается, что в случае, когда температура падает с высотой  еще быстрее, плотность воздуха растет с высотой. Однако такое состояние воздуха, очевидно, является сильно неустойчивым.

В нижних слоях атмосферы весьма часто имеют место градиенты температуры, значительно превосходящие сухоадиабатический. Обычно такие градиенты называют сверхадиабатическими. Чаще всего они наблюдаются до высот около 1 500 м, однако в некоторых случаях достигают высоты 3 000 м. Абсолютные значения сверхадиабатических градиентов от 1 до 1.5 градуса на 100 м. Однако в самом нижнем приземном слое градиент температуры может достигать во много раз больших значений.

Для перемещения воздушных масс и уничтожения неустойчивого равновесия требуются весьма значительные импульсы, которые не всегда имеются. Конечно, абсолютного покоя в атмосфере никогда не бывает. В частности, горизонтальный ветер сопровождается хотя бы малыми вертикальными движениями вследствие турбулентности. Но слабых движений воздуха может не хватить для быстрой ликвидации неустойчивого равновесия. Лишь при достаточной величине вертикальных смещений и при достаточной величине перемещающихся масс уничтожение неустойчивого равновесия становится возможным за небольшое время.