Сортування й пошук: Рецептурний довідник, страница 9

      Тепер ми бачимо, як виникає незбалансованість дерева. Якщо дані надходять у зростаючому порядку, кожний новий вузол додається праворуч від останнього вставленого. Це приводить до одного довгого списку. Зверніть увагу: чим більше “випадкові” дані, що надходять,, тим більше збалансованим виходить дерево.

      Видалення виробляються приблизно так само - необхідно тільки подбати про збереження структури дерева. Наприклад, якщо з дерева на мал. 3.4 віддаляється вузол 20, його спочатку потрібно замінити на вузол 37. Це дасть дерево, зображене на мал. 3.5. Міркування тут приблизно наступні. Нам потрібно знайти нащадка вузла 20, праворуч від якого розташовані вузли з більшими значеннями. Таким чином, нам потрібно вибрати вузол з найменшим значенням, розташований праворуч від вузла 20. Щоб знайти його, нам і потрібно спочатку спуститися на крок вправо (попадаємо у вузол 38), а потім на крок уліво (вузол 37); ці двухшаговые спуски тривають, поки ми не прийдемо в кінцевий вузол, аркуш дерева.

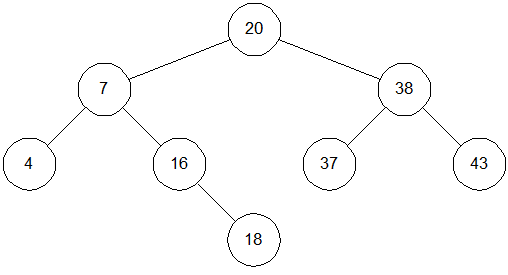
Рис. 0.4: Бінарне дерево після додавання вузла 18

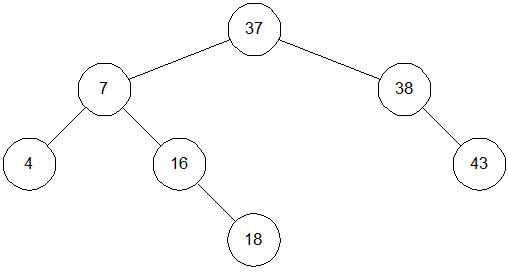
Рис. 0.5: Бінарне дерево після видалення вузла 20

Реалізація

Реалізація алгоритму на Си перебуває в розділі 4.6. Оператори typedef T і compGT варто змінити так, щоб вони відповідали даним, збереженим у дереві. Кожний вузол Node містить також покажчики left, right на лівого й правого нащадків, а також покажчик parent на предка. Властиво дані зберігаються в поле data. Адреса вузла, що є коренем дерева зберігається в укзателе root, значення якого на самому початку, природно, NULL. Функція insertNode запитує пам'ять під новий вузол і вставляє вузол у дерево, тобто встановлює потрібні значення потрібних покажчиків. Функція deleteNode, навпроти, видаляє вузол з дерева (тобто встановлює потрібні значення потрібних покажчиків), а потім звільняє пам'ять, що займав вузол. Функція findNode шукає в дереві вузол, що містить задане значення.

Двійкові дерева працюють найкраще, коли вони збалансовані, коли довжина шляху від кореня до кожного з листів перебуває в певних межах, пов'язаних із числом вузлів. Червоно-чорні дерева – один зі способів балансування дерев. Назва походить від стандартного розфарбування вузлів таких дерев у червоний і чорний кольори. Кольори вузлів використаються при балансуванні дерева. Під час операцій вставки й видалення поддеревья може знадобитися повернути, щоб досягти збалансованості дерева. Оцінкою як середнього час, так і найгіршого є O(lg n).

      Цей розділ – один з найбільш важких у даній книжці. Якщо ви очманієте від обертань дерев, спробуйте перейти до наступного розділу про розділені списки. Прекрасно написані розділи про червоно-чорні дерева ви знайдете в Кормена^[2].

Теорія

Червоно-чорне дерево – це бінарне дерево з наступними властивостями^[2]:

1.  Кожний вузол пофарбований або в чорний, або в червоні кольори.

2.  Листами оголошуються NIL-вузли (тобто “віртуальні” вузли, спадкоємці вузлів, які звичайно називають листами; на них “указують” NULL покажчики). Листи пофарбовані в чорні кольори.

3.  Якщо вузол червоний, то обоє його нащадка чорні.

4.  На всіх галузях дерева, ведучих від його кореня до листів, число чорних вузлів однаково.

Кількість чорних вузлів на галузі від кореня до аркуша називається чорною висотою дерева. Перераховані властивості гарантують, що сама довга галузь від кореня до аркуша не більш ніж удвічі длиннее будь-якої іншої галузі від кореня до аркуша. Щоб зрозуміти, чому це так, розглянемо дерево із чорною висотою 2. Найкоротша можлива відстань від кореня до аркуша дорівнює двом - коли обидва вузли чорні. Длиннейшее відстань від кореня до аркуша дорівнює чотирьом - вузли при цьому пофарбовані (від кореня до аркуша) так: червоний(чорний(червоний(чорний. Сюди не можна додати чорні вузли, оскільки при цьому порушиться властивість 4, з якого випливає коректність поняття чорної висоти. Оскільки відповідно до властивості 3 у червоних вузлів неодмінно чорні спадкоємці, у подібній послідовності неприпустимі й два червоних вузли підряд. Таким чином, длиннейший шлях, що ми можемо сконструювати, складається із чергування червоних і чорних вузлів, що й приводить нас до подвоєної довжини шляху, що проходить тільки через чорні вузли. Всі операції над деревом повинні вміти працювати з перерахованими властивостями. Зокрема, при вставці й видаленні ці властивості повинні зберегтися.