Сортування й пошук: Рецептурний довідник, страница 4

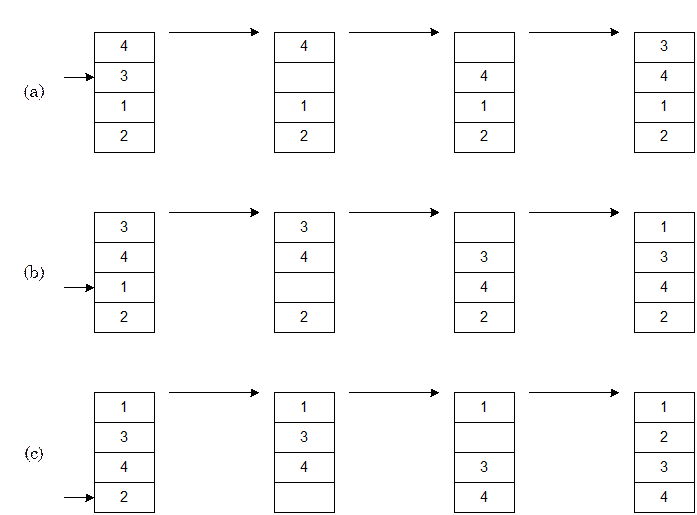
Рис. 0.1: Сортування вставками

Реалізація

Реалізацію сортування вставками на Си ви знайдете в розділі 4.1. Оператор typedef T і операторпорівняння compGT варто змінити так, щоб вони відповідали даним, збереженим у таблиці.

Метод, запропонований Дональдом Л. Шеллом, є нестійким сортуванням по місцю. Ефективність методу Шелла пояснюється тим, що елементи, що зрушують, швидко попадають на потрібні місця. Середній час для сортування Шелла рівняється O(n^1.25), для гіршого випадку оцінкою є O(n^1.5). Подальші посилання див. у книжці Батога ^[1].

Теория

На мал. 2.2(a) був наведений приклад сортування вставками. Ми спочатку виймали 1, потім зрушували 3 і 5 на одну позицію вниз, після чого вставляли 1. Таким чином, нам були потрібні два зрушення. Наступного разу нам було потрібно два зрушення, щоб вставити на потрібне місце 2. На весь процес нам було потрібно 2+2+1=5 зрушень.

На мал. 2.2(b) ілюструється сортування Шелла. Ми починаємо, роблячи сортування вставками із кроком 2. Спочатку ми розглядаємо числа 3 і 1: витягаємо 2, зрушуємо 3 на 1 позицію із кроком 2, вставляємо 2. Потім повторюємо те ж для чисел 5 і 2: витягаємо 2, зрушуємо вниз 5, вставляємо 2. І т.д. Закінчивши сортування із кроком 2, робимо її із кроком 1, тобто виконуємо звичайне сортування вставками. Усього при цьому нам знадобиться 1 + 1+ 1 = 3 зрушення. Таким чином, використавши спочатку крок, більший 1, ми домоглися меншого числа зрушень.

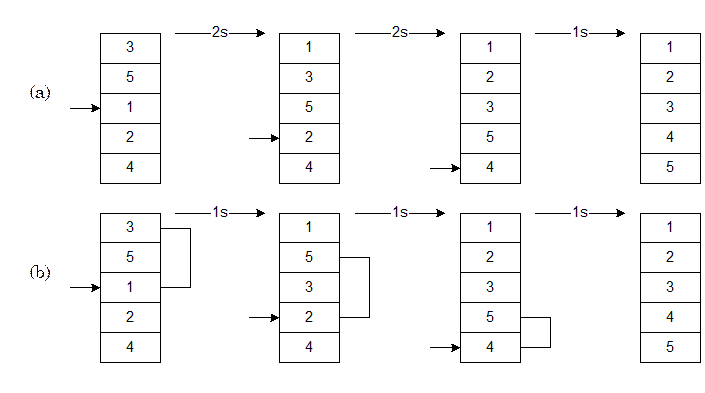
Рис. 0.2: Сортування Шелла

Можна використати самі різні схеми вибору кроків. Як правило, спочатку ми сортуємо масив з більшим кроком, потім зменшуємо крок і повторюємо сортування. У самому кінці сортуємо із кроком 1. Хоча цей метод легко пояснити, його формальний аналіз досить важкий. Зокрема, теоретикам не вдалося знайти оптимальну схему вибору кроків. Батіг^[1] провів безліч експериментів і наступну формулу вибору кроків (h) для масиву довжини N:

От трохи перших значень h:

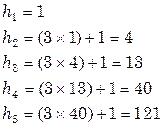
Щоб відсортувати масив довжиною 100, насамперед знайдемо номер s, для якого h_s ³ 100. Відповідно до наведених цифр, s = 5. Потрібне нам значення перебуває двома рядками вище. Таким чином, послідовність кроків при сортуванні буде такою: 13-4-1. Ну, звичайно, нам не потрібно зберігати цю послідовність: чергове значення h перебуває з попередні по формулі

Реалізація

Реалізацію сортування Шелла на Си ви знайдете в розділі 4.2. Оператор typedef T і операторпорівняння compGT варто змінити так, щоб вони відповідали даним, збереженим у масиві. Основна частина алгоритму – сортування вставками із кроком h.

Хоча ідея Шелла значно поліпшує сортування вставками, резерви ще залишаються. Один з найбільш відомих алгоритмів сортування - швидке сортування, запропоноване Ч.Хоором. Метод і справді дуже швидкий, недарма по-англійському його так і величають QuickSort до невдоволення всіх спелл-чекеров (“...Шишков прости: не знаю, як перевести”).

Цьому методу потрібно O(n lg n) у середньому й O(n²) у найгіршому разі. На щастя, якщо прийняти адекватні обережності, найгірший випадок украй малоймовірний. Швидкий пошук не є стійким. Крім того, йому потрібно стек, тобто він не є й методом сортування на місці. Подальшу інформацію можна одержати в роботі Кормена ^[2].

Теорія

Алгоритм розбиває сортируемый масив на розділи, потім рекурсивно сортує кожний розділ. У функції Partition (Рис. 0.3) один з елементів масиву вибирається в якості центрального. Ключі, менші центрального варто розташувати ліворуч від нього, ті, які більше, - праворуч.

Рис. 0.3: Швидкий пошук