Сортування й пошук: Рецептурний довідник, страница 5

На малий. 2.4 (a) у якості центрального обраний елемент 3. Індекси починають змінюватися з кінців масиву. Індекс i починається ліворуч і використається для вибору елементів, які більше центрального, індекс j починається праворуч і використається для вибору елементів, які менше центрального. Ці елементи міняються місцями – див. мал. 2.4 (b). Процедура QuickSort рекурсивно сортує два подмассива, у результаті виходить масив, представлений на мал. 2.4 (c).

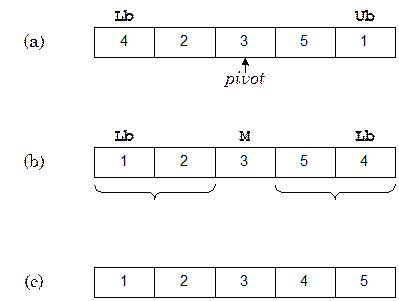
Рис. 0.4: Приклад роботи алгоритму Quicksort

У процесі сортування може знадобитися пересунути центральний елемент. Якщо нам повезе, обраний елемент виявиться медіаною значень масиву, тобто розділить його навпіл. Припустимо на хвилинку, що це й справді так. Оскільки на кожному кроці ми ділимо масив навпіл, а функція Partition зрештою перегляне всі n елементів, час роботи алгоритму є O(n lg n).

В якості центрального функція Partition може попросту брати перший елемент (A[Lb]). Всі інші елементи масиву ми порівнюємо із центральним і пересуваємо або вліво від нього, або вправо. Є, однак, один випадок, що безжалісно руйнує цю прекрасну простоту. Припустимо, що наш масив із самого початку відсортований. Функція Partition завжди буде одержувати в якості центрального мінімальний елемент і тому розділить масив найгіршим способом: у лівому розділі виявиться один елемент, відповідно, у правом залишиться Ub – Lb елементів. Таким чином, кожний рекурсивний виклик процедури quicksort усього лише зменшить довжину сортируемого масиву на 1. У результаті для виконання сортування знадобиться n рекурсивних викликів, що приводить до часу роботи алгоритму порядку O(n²). Один зі способів побороти цю проблему – випадково вибирати центральний елемент. Це зробить найгірший випадок надзвичайно малоймовірним.

Реалізація

Реалізація алгоритму на Си перебуває в розділі 4.3. Оператори typedef T і compGT варто змінити так, щоб вони відповідали даним, збереженим у масиві. У порівнянні з основним алгоритмом є деякі поліпшення::

• У якості центрального у функції partition вибирається елемент, розташований у середині. Такий вибір поліпшує оцінку середнього часу роботи, якщо масив упорядкований лише частково. Найгірша для цієї реалізації ситуація виникає у випадку, коли щораз при роботі partition.у якості центрального вибирається максимальний або мінімальний елемент.
• Для коротких масивів викликається insertSort. Через рекурсію й інших “накладних витрат” швидкий пошук виявляється не настільки вуж швидким для коротких масивів. Тому, якщо в масиві менше 12 елементів, викликається сортування вставками. Граничне значення не критично - воно сильно залежить від якості генерируемого коду.
• Якщо останній оператор функції є викликом цієї функції, говорять про хвостову рекурсію. Її має сенс заміняти на ітерації – у цьому випадку краще використається стек. Це зроблено при другому виклику QuickSort на мал. 2.3.
• Після розбивки спочатку сортується менший розділ. Це також приводить до кращого використання стека, оскільки короткі розділи сортуються швидше і їм потрібний більше короткий стек.

У розділі 4.4 ви знайдете також qsort – функцію зі стандартної бібліотеки Си, що, у відповідності назвою, заснована на алгоритмі quicksort. Для цієї реалізації рекурсія була замінена на ітерації. У таблиці 2.1 приводиться час і розмір стека, затрачувані до й після описаних поліпшень.

Таблиця 0.1:  Вплив поліпшень на швидкість роботи й розмір стека

У даному розділі мі порівнавним описані алгоритми сортування: вставками, Шелла й швидке сортування. Є трохи факторів, що впливають на вибір алгоритму в кожній конкретній ситуації: