Сортування й пошук: Рецептурний довідник, страница 6

• Стійкість. Нагадаємо, що стійке сортування не міняє взаємного розташування елементів з рівними ключами. Сортування вставками - єдиний з розглянутих алгоритмів, що володіють цією властивістю.
• Пам'ять. Сортуванню на місці не потрібна додаткова пам'ять. Сортування вставками й Шелла задовольняють цій умові. Швидкому сортуванню потрібно стек для організації рекурсії. Однак, необхідне цьому алгоритму місце можна сильно зменшити, повозившись із алгоритмом.
• Час. Час, потрібне для сортування наших даних, легко стає астрономічним (див. таблицю 1.1). Таблиця 2.2 дозволяє зрівняти тимчасові витрати кожного з алгоритмів по кількості операторів, що виконують..

Таблиця 0.2:Порівняння методів сортування

• Час, витрачений кожним з алгоритмів на сортування випадкового набору даних, представлено в таблиці 2.3.

Таблиця 0.3: Час сортування

3. Словники

Для роботи зі словником потрібні пошук, вставка й видалення. Один з найбільш ефективних способів реалізації словника – хеш-таблицы. Середній час пошуку елемента в них є O(1), час для найгіршого випадку – O(n). Прекрасний виклад хеширования можна знайти в роботах Кормена^[2] і Батоги^[1]. Щоб читати статті на цю тему, вам знадобиться володіти відповідною термінологією. Тут описаний метод, відомий як зв'язування або відкрите хеширование^[3]. Інший метод, відомий як замкнуте хеширование^[3] иëè заêðûòàÿ адресація^[1], тут не обговорюються. Ну, як?

Теорія

Хеш-таблица – це звичайний масив з незвичайною адресацією, що задає хеш-функцией. Наприклад, на hashTable мал. 3.1 – це масив з 8 елементів. Кожний елемент являє собою покажчик на лінійний список, що зберігає числа. Хеш-функция в цьому прикладі просто ділить ключ на 8 і використає залишок як індекс у таблиці. Це дає нам числа від 0 до 7 Оскільки для адресації в hashTable нам і потрібні числам від 0 до 7, алгоритм гарантує припустимі значення індексів.

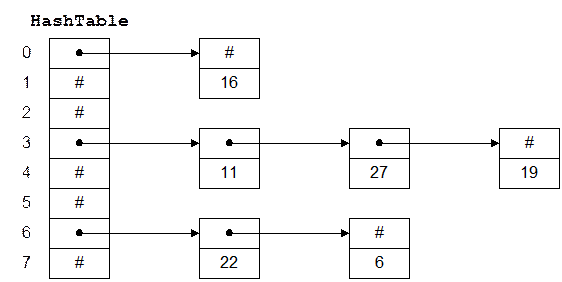
Рис. 0.1: Хеш-таблица

Щоб вставити в таблицю новий елемент, мі хешируем ключ, щоб визначити список, у який його потрібно додати, потім вставляємо елемент у початок цього списку. Наприклад, щоб додати 11, ми ділимо 11 на 8 і одержуємо залишок 3. Таким чином, 11 варто розмістити в списку, на початок якого вказує hashTable[3]. Щоб знайти число, ми його хешируем і проходимо по відповідному списку. Щоб видалити число, ми знаходимо його й видаляємо елемент списку, його утримуючий.

Якщо хеш-функция розподіляє сукупність можливих ключів рівномірно по безлічі індексів, то хеширование ефективно розбиває безліч ключів. Найгірший випадок – коли всі ключі хешируются в один індекс. При цьому ми працюємо з одним лінійним списком, що і змушені послідовно сканувати щораз, коли що-небудь робимо. Звідси видно, як важлива гарна хеш-функция. Тут ми розглянемо лише трохи з можливих підходів. При ілюстрації методів передбачається, що unsigned char розташовується в 8 бèòах, unsigned short int – в 16, unsigned long int – в 32.

·  Розподіл (розмір таблиці hashTableSize – простої число). Цей метод використаний в останньому прикладі. Хеширующее значення hashValue, що змінюється від 0 до (hashTableSize - 1), дорівнює залишку від розподілу ключа на розмір хеш-таблицы. От як це може виглядати:

typedef int hashIndexType;

hashIndexType hash(int Key) {
    return Key % hashTableSize;
 }