Сортування й пошук: Рецептурний довідник, страница 10

Вставка

Щоб вставити вузол, ми спочатку шукаємо в дереві місце, куди його варто додати. Новий вузол завжди додається як аркуш, тому обоє його нащадка є NIL-вузлами й передбачаються чорними. Після вставки красимо вузол у червоні кольори. Після цього дивимося на предка й перевіряємо, чи не порушується червоно-чорна властивість. Якщо необхідно, ми перефарбовуємо вузол і робимо поворот, щоб збалансувати дерево.

      Вставивши червоний вузол, ми зберігаємо властивість чорної висоти (властивість 4). Однак, при цьому може виявитися порушеним властивість 3. Ця властивість полягає в тому, що обоє нащадка червоного вузла обов'язково чорні. У нашому випадку обоє нащадка нового вузла чорні по визначенню (оскільки вони є NIL-вузлами), так що розглянемо ситуацію, коли предок нового вузла червоний: при цьому буде порушена властивість 3. Досить розглянути наступні два випадки:

• Червоний предок, червоний “дядько”. Ситуацію червоний-червоний ілюструє мал. 3.6. У нового вузла  X предок і “дядько” виявилися червоними. Просте перефарбування рятує нас від червоно-червоного порушення. Після перефарби потрібно перевірити “дідуся” нового вузла (вузол B), оскільки він може виявитися червоним. Зверніть увагу на поширення впливу червоного вузла на верхні вузли дерева. У самому кінці корінь ми красимо в чорні кольори корінь дерева. Якщо він був червоним, то при цьому збільшується чорна висота дерева.
• Червоний предок, чорний “дядько”. На мал. 3.7 представлений інший варіант червоно-червоного порушення - “дядько” нового вузла виявився чорним. Тут вузли може знадобитися обертати, щоб скорегувати поддеревья. У цьому місці алгоритм може зупинитися через відсутність червоно-червоних конфліктів і вершина дерева (вузол A) офарблюється в чорні кольори. Зверніть увагу, що якщо вузол X був на початку правим нащадком, те першим застосовується ліве обертання, що робить цей вузол лівим нащадком.

Кожне коректування, вироблене при вставці вузла, змушує нас здійнятися в дереві на один крок. У цьому випадку до зупинки алгоритму буде зроблене 1 обертання (2, якщо вузол був правим нащадком). Метод видалення аналогічний.

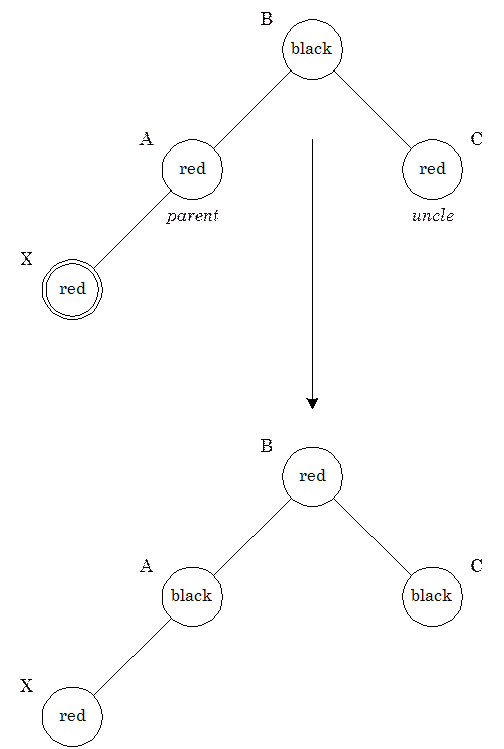
Рис. 0.6: Вставка – Червоний предок, червоний “дядько”

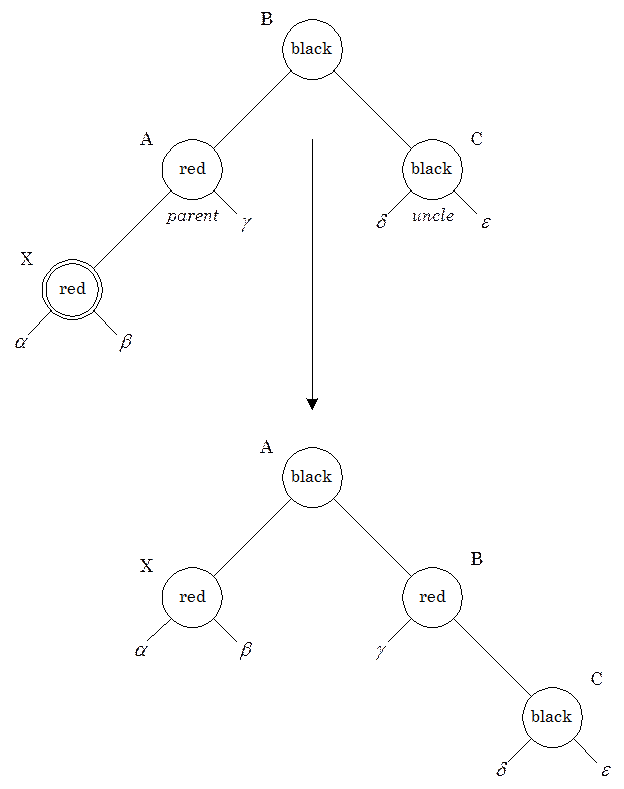
Рис. 0.7: Вставка – червоний предок, чорний “дядько”

Реалізація

Реалізація роботи із червоно-чорними деревами на Си перебуває в розділі 4.7. Оператори typedef T, а також порівнюють compLT і compEQ варто змінити так, щоб вони відповідали даним, збереженим у вузлах дерева. У кожному вузлі Node зберігаються покажчики left, right на двох нащадків і parent на предка. Кольори вузла зберігається в поле color і може бути або RED, або BLACK. Властиво дані зберігаються в поле data. Всі листи дерева є “сторожовими” (sentinel), що сильно спрощує коди. Вузол root є коренем дерева й на самому початку є сторожовим.

      Функція insertNode запитує пам'ять під новий вузол, установлює потрібні значення його полий і вставляє в дерево. Відповідно, вона викликає insertFixup, що стежить за збереженням червоно-чорних властивостей. Функція deleteNode видаляє вузол з дерева. Вона викликає deleteFixup, що відновлює червоно-чорні властивості. Функція findNode шукає в дереві потрібний вузол.

Розділені списки – це зв'язні списки, які дозволяють вам стрибнути (skip) до потрібного елемента. Це дозволяє перебороти обмеження послідовного пошуку, що є основним джерелом неефективного пошуку в списках. У той же час вставка й видалення залишаються порівняно ефективними. Оцінка середнього часу пошуку в таких списках є O(lg n). Для найгіршого випадку оцінкою є O(n), але гірший випадок украй малоймовірний. Відмінне введення в розділені списки ви знайдете в П'ю ^[5].

Теорія

Ідея, що лежить в основі розділених списків, дуже нагадує метод, використовуваний при пошуку імен в адресній книжці. Щоб знайти ім'я, ви позначаєте буквою сторінку, звідки починаються імена, що починаються із цієї букви. На мал. 3.8, наприклад, самий верхній список представляє звичайний однозв'язний список. Додавши один “рівень” посилань, ми прискоримо пошук. Спочатку ми підемо по посиланнях рівня 1, потім, коли дійдемо по потрібного відрізка списку, підемо по посиланнях нульового рівня.