Сортування й пошук: Рецептурний довідник, страница 2

Лютий 1998

1. Введення

Пошук, вставка й видалення, як відомо, – основні операції при роботі з даними. Ми почнемо з дослідження того, як ці операції реалізуються над самі відомими об'єктами - масивами й (зв'язаними) списками.

Масиви

На мал. 1.1 показаний масив із семи елементів із числовими значеннями. Щоб знайти в ньому потрібне нам число, ми можемо використати лінійний пошук – його алгоритм наведений на мал. 1.2. Максимальне число порівнянь при такому пошуку – 7; воно досягається у випадку, коли потрібне нам значення перебуває в елементі A[6]. Якщо відомо, що дані відсортовані, можна застосувати двійковий пошук (мал. 1.3). Змінні Lb і Ub містять, відповідно, ліву й праву границі відрізка масиву, де перебуває потрібний нам елемент. Ми починаємо завжди з дослідження середнього елемента відрізка. Якщо шукане значення менше середнього елемента, ми переходимо до пошуку у верхній половині відрізка, де всі елементи менше тільки що перевіреного. Інакше кажучи, значенням Ub стає (M – 1) і на наступній ітерації ми працюємо з половиною масиву. Таким чином, у результаті кожної перевірки ми двоє звужуємо область пошуку. Так, у нашому прикладі, після першої ітерації область пошуку - усього лише три елементи, після другої залишається всього лише один елемент. Таким чином, якщо довжина масиву дорівнює 6, нам досить трьох ітерацій, щоб знайти потрібне число.

Рис. 0.1:  Масив

Двійковий пошук - дуже потужний метод. Якщо, наприклад, довжина масиву дорівнює 1023, після першого порівняння область звужується до 511 елементів, а після другий – до 255. Легко порахувати, що для пошуку в масиві з 1023 елементів досить 10 порівнянь.

Крім пошуку нам необхідно буває вставляти й видаляти елементи. На жаль, масив погано пристосований для виконання цих операцій. Наприклад, щоб вставити число 18 у масив на мал. 1.1, нам знадобиться зрушити елементи A[3]…A[6] униз – лише після цього ми зможемо записати число 18 в елемент A[3]. Аналогічна проблема виникає при видаленні елементів. Для підвищення ефективності операцій вставки/видалення запропоновані зв'язані списки.

Рис. 0.2:  Лінійний пошук

Рис. 0.3:  Двійковий пошук

Однозв'язні списки

На малий. 1.4 ті ж числа, що й раніше, зберігаються у вигляді зв'язаного списку; слово “зв'язаний” часто опускають. Припускаючи, що X і P є покажчиками, число 18 можна вставити в такий список у такий спосіб:

X->Next = P->Next;

P->Next = X;

Списки дозволяють здійснити вставку й видалення дуже ефективно. Поцікавимося, однак, як знайти місце, куди ми будемо вставляти новий елемент, тобто яким образом привласнити потрібне значення покажчику P. На жаль, для пошуку потрібної крапки прийде пройтися по елементах списку. Таким чином, перехід до списків дозволяє зменшити час вставки/видалення елемента за рахунок збільшення часу пошуку.

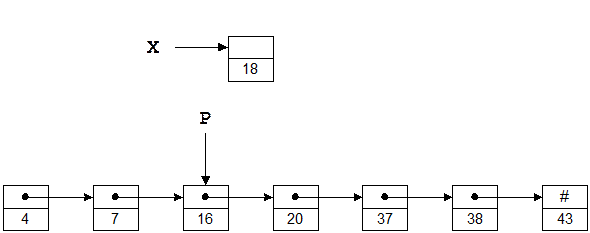
Рис. 0.4: Однозв'язний список

Оцінки часу виконання