Сортування й пошук: Рецептурний довідник, страница 8

      Розмір хеш-таблицы повинен бути досить великий, щоб у ній залишалося розумне число порожніх місць. Як видно з таблиці 3.1, чим менше таблиця, тим більше середній час пошуку ключа в ній. Хеш-таблицу можна розглядати як сукупність зв'язаних списків. У міру того, як таблиця росте, збільшується кількість списків і, відповідно, середнє число вузлів у кожному списку зменшується. Нехай кількість елементів дорівнює n. Якщо розмір таблиці дорівнює 1, то таблиця вироджується в один список довжини n. Якщо розмір таблиці дорівнює 2 і хеширование ідеально, то нам оведеться мати справа із двома списками по n/100 елементів у кожному. Як ми бачимо в таблиці 3.1, є значна волі у виборі довжини таблиці.

Таблиця 0.1: Залежність середнього часу пошуку (ms) від   hashTableSize.
Сортуються 4096 елементів.

Реалізація

Реалізація алгоритму на Си перебуває в розділі 4.5. Оператори typedef T і compGT варто змінити так, щоб вони відповідали даним, збереженим у масиві. Для роботи програми варто також визначити hashTableSize і відвести місце під hashTable. У хеш-функции hash використаний метод розподілу. Функція insertNode відводить пам'ять під новий вузол і вставляє його в таблицю. Функція deleteNode видаляє вузол і звільняє пам'ять, де він розташовувався. Функція findNode шукає в таблиці заданий ключ.

У розділі 1 ми використали двійковий пошук для пошуку даних у масиві. Цей метод надзвичайно ефективний, оскільки кожна ітерація вдвічі зменшує число елементів, серед яких нам потрібно продовжувати пошук. Однак, оскільки дані зберігаються в масиві, операції вставки й видалення елементів не настільки ефективні. Двійкові дерева дозволяють зберегти ефективність всіх трьох операцій – якщо робота йде з “випадковими” даними. У цьому випадку час пошуку оцінюється як O(lg n). Найгірший випадок – коли уставляються впорядковані дані. У цьому випадку оцінка час пошуку – O(n). Подробиці ви знайдете в роботі Кормена ^[2].

Теорія

Двійкове дерево – це дерево, у якого кожний вузол має не більше двох спадкоємців. Приклад бінарного дерева наведений на мал. 3.2. Припускаючи, що Key містить значення, збережене в даному вузлі, ми можемо сказати, що бінарне дерево має наступну властивість: у всіх вузлів, розташованих ліворуч від даного вузла, значення відповідного поля менше, ніж Key, у всіх вузлів, розташованих праворуч від нього, – більше. Вершину дерева називають його коренем, вузли, у яких відсутні обоє спадкоємця, називаються листами. Корінь дерева на мал. 3.2 містить 20, а листи – 4, 16, 37 і 43. Висота дерева – це довжина наидлиннейшего зі шляхів від кореня до листів. У нашому прикладі висота дерева дорівнює 2.

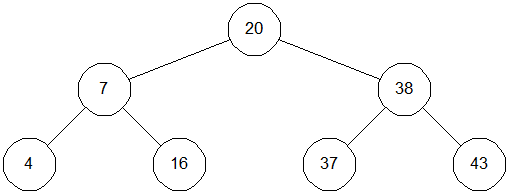
Рис. 0.2: Двійкове дерево

      Щоб знайти в дереві якесь значення, ми стартуємо з кореня й рухаємося вниз. Наприклад, для пошуку числа 15, ми зауважуємо, що 16 ( 20, і тому йдемо вліво. При другому порівнянні маємо 16 ( 7,  так що ми рухаємося вправо. Третя спроба успішна - ми знаходимо елемент із ключем, рівним 15.

      Кожне порівняння вдвічі зменшує кількість елементів, що залишилися. Щодо цього алгоритм схожий на двійковий пошук у масиві. Однак, все це вірно тільки у випадках, коли наше дерево збалансоване. На мал. 3.3 показане інше дерево, що містить ті ж елементи. Незважаючи на те, що це дерево теж бінарне, пошук у ньому схожий, скоріше, на пошук в однозв'язному списку, час пошуку збільшується пропорційно числу елементів, що запам'ятовують.

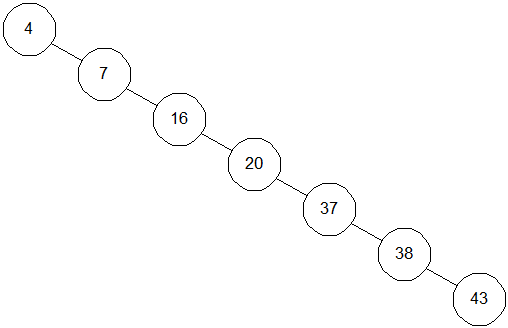
Рис. 0.3: Незбалансоване бінарне дерево

Вставка й видалення

Щоб краще зрозуміти, як дерево стає незбалансованим, подивимося на процес вставки пристальнее. Щоб вставити 18 у дерево на мал. 3.2 ми шукаємо це число. Пошук приводить нас у вузол 16, де благополучно завершується. Оскільки 18 ( 16, ми попросту додає вузол 18 як правий нащадок вузла 16 (мал. 3.4).