Основы работы в MathCAD, страница 6

Пиктограмма	в панели инструментов Calculator (Калькулятор)  в панели инструментов Matrix (Матрица)
Клавиатура	клавиши  "*"

На Рис. 2.8 приведен пример умножения матриц.

Транспонирование матрицы

Транспонированием называется матричная операция, переводящая матрицу размером MxN в матрицу размером NxM, путем перестановки строк и столбцов с одинаковыми индексами.

Варианты ввода операции транспонирования.

Пиктограмма	в панели инструментов Matrix (Матрица)
Клавиатура	клавиши  "Ctrl"+"1"

На Рис. 2.9 приведен пример транспонирования матрицы.

Определитель матрицы

Варианты ввода операции расчета определителя матрицы.

Пиктограмма	в панели инструментов Matrix (Матрица)
Клавиатура	клавиши  "Shift"+"|"

На Рис. 2.9 приведен пример вычисления определителя матрицы.

Рис. 2.9. Операции умножения и сложения матриц

Модуль вектора

Модуль вектора равен квадратному корню из суммы квадратов его элементов

Варианты ввода операции модуля вектора.

Пиктограмма	в панели инструментов Matrix (Матрица)
Клавиатура	клавиши  "Shift"+"|"

На Рис. 2.9 приведен пример вычисления модуля вектора.

Обратная матрица

Матрица M^-1 называется обратной к матрице М, если
М*М^-1=Е, где Е- единичная матрица.

Матрица имеет обратную только в том случае если она квадратная и ее определитель не равен нулю.

Варианты ввода операции обратной матрицы.

Пиктограмма	в панели инструментов Matrix (Матрица)
Клавиатура	клавиши  "Shift"+"^" и ввести в показатель степени число -1
Функция	geninv(M), М – квадратная матрица с не нулевым определителем

На Рис. 2.9 приведен пример вычисления обратной матрицы.

Рис. 2.10. Операции транспонирования, обратной матрицы и ее определителя и получения модуля вектора

Векторное произведение векторов

Векторным произведением называется вектор, длина которого равна произведению длин исходных векторов и синуса угла между ними, а направление его совпадает с направлением перпендикуляра к плоскости этих двух векторов (по правилу "буравчика").

Варианты ввода операции векторного произведения векторов.

Пиктограмма	в панели инструментов Matrix (Матрица)
Клавиатура	клавиши  "Shift"+"|"

На Рис. 2.10 приведен пример векторного произведения векторов.

Скалярное произведение векторов

Скалярным произведением векторов называется число (или выражение), равное произведению длин перемножаемых векторов и косинуса угла между ними.

Варианты ввода операции скалярного произведения векторов.

Пиктограмма	в панели инструментов Calculator (Калькулятор)  в панели инструментов Matrix (Матрица)
Клавиатура	клавиши  "*"

На Рис. 2.10 приведен пример скалярного произведения векторов.

Суммирование элементов вектора

Варианты ввода операции суммирования элементов вектора.

Пиктограмма	в панели инструментов Matrix (Матрица)
Клавиатура	клавиши  "Ctrl"+"4"

На Рис. 2.10 приведен пример суммирования элементов вектора.

Рис. 2.11. Операции векторного и скалярного умножения векторов и суммирование элементов вектора

3  Исследование систем линейных алгебраических уравнений в пакете MathCAD

Пример №1.

Задание. Показать, что столбцы 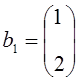 и 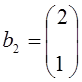, составленные из коэффициентов уравнений

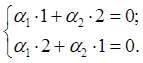
 являются линейно независимыми.

______________________________________________________

Последовательность действий.

1. Ввести сопроводительный текст "Пример №1" в правом верхнем углу листа.

Установить шрифт - MS Sans Serif сопроводительного текста, поддерживающий кириллицу. Для этого надо модифицировать текстовый стиль "Normal":