Кинематический и динамический анализы простых четырехзвенных механизмов, страница 2

Существуют общие закономерности в структуре (строении) различных механизмов, связывающие число степеней свободы W механизма с числом звеньев и числом и видом кинематических пар. Эти закономерности носят название структурных формул механизмов. Наиболее общей является структурная формула Сомова – Малышева, которую можно использовать для определения степени подвижности любого механизма:

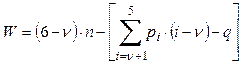,                               (9.1)

где n– число подвижных звеньев; v – число общих ограничений, накладываемых на движение звеньев, например, для пространственных механизмов , для плоских механизмов ; () ·n – число степеней свободы всех звеньев механизма, без наложенных на них связей (ограничений) кинематическими парами;  – количество кинематических пар i-го класса; i – класс кинематической пары; q – число избыточных связей; в квадратных скобках – число связей накладываемых кинематическими парами на относительное движение звеньев.

Подставляя в формулу (9.1) , получим структурную формулу для плоских механизмов без учета пассивных связей (формула Чебышева):

;

где  – число кинематических пар пятого класса;  – число кинематических пар четвертого класса.

Определим степень подвижности механизмов, изображенных на рис. 9.2 по формуле Чебышева:

– рис. 9.2, а

– рис. 9.2, б

– рис. 9.9, в

– рис. 9.2, г

– рис. 9.2, д

– рис. 9.2, е

.

Полученные значения степени подвижности W указывают на количество ведущих звеньев или приводов, необходимых для приведения механизма в действие.

9.1.4. Избыточные связи

Кроме связей, активно влияющих на число степеней свободы механизмов (степень подвижности), могут встретиться степени свободы и условия связи, не оказывающие влияния на характер движения механизма в целом. Удаление из механизмов звеньев и кинематических пар, которым принадлежат эти степени свободы и условия связи, может быть сделано без изменения степени подвижности механизмов. Такие степени свободы называют лишними степенями свободы, а связи – избыточными (пассивными) связями.

Избыточные связи не изменяют подвижность механизма, только превращают его в статически неопределимую систему. При отсутствии избыточных связей () сборка механизма происходит без деформации звеньев, которые как бы самоустанавливаются. Поэтому такие механизмы называют самоустанавливающимися.

При наличии избыточных связей (q > 0) сборка механизма и движение его звеньев становятся возможными только при деформации последних. Поэтому такие механизмы требуют повышенной точности изготовления. В противном случае деформации звеньев при сборке вызывают дополнительное нагружение звеньев и кинематических пар, сверх тех нагрузок, для передачи которых предназначен механизм. Кроме того, трение в кинематических парах может значительно увеличиться и привести к заклиниванию механизма.

Рис. 9.2. Структурные схемы механизмов

В ряде случаев сознательно проектируют механизмы с избыточными связями для решения следующих задач:

– обеспечение требуемой прочности звеньев за счет перераспределения нагрузки;

– получение требуемой жесткости звеньев;

– уменьшение износа элементов кинематических пар;

– получение определенности движения звеньев механизма при прохождении крайних положений.

На рис. 9.3 показана кинематическая цепь, которая в общем случае представляет собой ферму с нулевой подвижностью:

.

При , ,  наличие звена 4 не изменяет характера движения шарнирного четырехзвенника ABCD. Реально существующий механизм параллельных кривошипов имеет одну степень подвижности, т.е. одно ведущее звено:

.

Если из схемы удалить звено 4, относительное движение остальных звеньев сохранится прежним. Поэтому связи E и F являются избыточными. Звено 4 включено в схему для получения определенности движения звеньев механизма при прохождении крайних положений.

Высшая кинематическая пара четвертого класса р₄ может быть заменена введением в схему механизма дополнительного звена и двух низших кинематических па пятого класса р₅.