Глава 3. СИНТЕЗ САМОНАСТРАИВАЮЩИХСЯ РЕГУЛЯТОРОВ НЕЛИНЕЙНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
3.1. Постановка задачи адаптивного управления
Апостериорная модель объекта управления. Рассматривается задача синтеза адаптивной системы автоматического управления нелинейным объектом, которая содержит (рис. 3.1) систему само-настраивающихся регуляторов управляющих воздействий (СРУВ), объект управления (ОУ), измерительные устройства (ИУ) и наблю-датель переменных состояния объекта управления (НПСОУ).
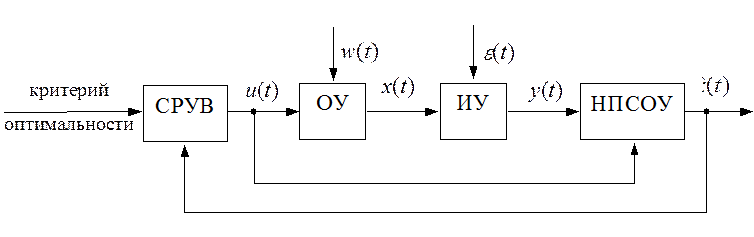
Рис. 3.1. Функциональная схема адаптивной системы автоматического управления
Объект управления (ОУ) имеет следующее уравнение состояния:
|
|
(3.1.1) |
с заданными начальными условиями
|
|
(3.1.2) |
где ![]() и
и ![]() – векторы оптимальных оценок переменных
состояния объекта управления и возмущающих воздействий;
– векторы оптимальных оценок переменных
состояния объекта управления и возмущающих воздействий; ![]() –
вектор известных функций, определенных при решении задачи синтеза наблюдателя
переменных состояния ОУ;
–
вектор известных функций, определенных при решении задачи синтеза наблюдателя
переменных состояния ОУ; ![]() - вектор управляющих воздействий.
- вектор управляющих воздействий.
Наблюдатель переменных состояния объекта управления формирует оценки ![]() вектора переменных состояния ОУ и оценки
вектора переменных состояния ОУ и оценки ![]() вектора возмущающих воздействий
вектора возмущающих воздействий ![]() по алгоритму, разработанному в разделе 2.3.
По линии обратной связи оценки
по алгоритму, разработанному в разделе 2.3.
По линии обратной связи оценки ![]() вектора переменных
состояния ОУ поступают в многомерный самонастраивающийся регулятор управляющих
воздействий, который формирует управляющие воздействия, оптимальные по
используемому критерию.
вектора переменных
состояния ОУ поступают в многомерный самонастраивающийся регулятор управляющих
воздействий, который формирует управляющие воздействия, оптимальные по
используемому критерию.
Модель допустимых управляющих воздействий. Множество допустимых управляющих воздействий задано уравнениями (2.1.13)-(2.1.15):
|
|
|
|
с начальными условиями
|
|
где ![]() – вектор, образованный белыми
шумами
– вектор, образованный белыми
шумами ![]() с нулевыми средними значениями и матрицей
интенсивностей
с нулевыми средними значениями и матрицей
интенсивностей
|
|
(3.1.3) |
Ограничения на фазовые траектории и конечное состояние объекта управления. Обычно с помощью управляющих воздействий требуется перевести объект управления из начального состояния (3.1.2) в заданное конечное состояние при некоторых ограничениях.
Так, например, иногда требуется за минимальное время перевести объект управления в новое установившееся состояние, в котором
|
|
(3.1.4) |
где ![]() - вектор заданных значений части переменных состояния в момент времени
- вектор заданных значений части переменных состояния в момент времени ![]() ;
; ![]() - вектор допустимых погрешностей управления.
- вектор допустимых погрешностей управления.
При этом множество допустимых траекторий перехода из начального состояния в конечное состояние обычно задают с помощью ограничений в виде неравенств
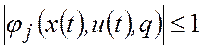 ,
,
![]() ,
,
которые должны выполняться с заданными допустимыми
погрешностями ![]() . Эти неравенства, как это было
показано ранее, можно заменить с требуемой точностью нелинейными уравнениями
. Эти неравенства, как это было
показано ранее, можно заменить с требуемой точностью нелинейными уравнениями
|
|
(3.1.5) |
В общем случае ограничения на допустимые фазовые траектории переменных состояния и конечное состояние объекта управления можно задать, объединив, например, условия (3.1.4) и (3.1.5), нелинейным уравнением
|
|
(3.1.6) |
где ![]() – вектор известных функций,
определяющих допустимые фазовые траектории перехода части переменных состояния
из начального состояния в заданное конечное состояние.
– вектор известных функций,
определяющих допустимые фазовые траектории перехода части переменных состояния
из начального состояния в заданное конечное состояние.
Допустимые погрешности управления ![]() обычно можно
считать случайными процессами с ковариационными функциями
обычно можно
считать случайными процессами с ковариационными функциями
|
|
(3.1.7) |
Как было показано в разделе 2.1.4, уравнение (3.1.6), определя-ющее допустимые фазовые траектории с такими погрешностями, можно преобразовать, используя скользящее временное окно, в эквивалентное уравнение
|
|
(3.1.8) |
где
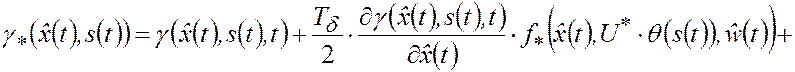
|
|
(3.1.9) |
![]() - вектор
белых шумов с нулевыми средними значениями и матрицей интенсивностей
- вектор
белых шумов с нулевыми средними значениями и матрицей интенсивностей
|
|
(3.1.10) |
Таким образом, математическую модель системы управления, предназначенную для использования при формировании управляющих воздействий, определяют уравнения (3.1.1)-(3.1.3), (2.1.13)-(2.1.15), (3.1.8)-(3.1.10). Эта модель отличается от традиционных моделей систем управления тем, что множество допустимых управляющих воздействий задано с помощью системы нелинейных алгебраических и линейных дифференциальных уравнений (2.1.13)-(2.1.15) для дополнительных вспомогательных переменных. В эти уравнения входят линейным образом неизвестные случайные переменные типа белого шума. Исходные ограничения на фазовые траектории в виде неравенств и уравнения, задающие конечное состояние объекта управления, преобразованы в этой модели в систему нелинейных алгебраических уравнений (3.1.8)-(3.1.10), которые определяют множество допустимых фазовых траекторий для части переменных состояния объекта управления.
3.2. Критерии эффективности управления
Критерий максимума апостериорной вероятности. Пусть начальные условия (3.1.2), (2.1.15) являются гауссовскими случайными величинами, а
отклонения ![]() фазовых траекторий от заданных траекторий
(3.1.6) имеют гауссовские функции распреде-ления. Кроме того, пусть белые шумы
фазовых траекторий от заданных траекторий
(3.1.6) имеют гауссовские функции распреде-ления. Кроме того, пусть белые шумы ![]() , из которых формируют допустимые
управляющие воздействия, имеют гауссовские функции распределения. В этом случае
можно сформировать генератор управляющих воздействий, оптимальный по критерию
МАВ.
, из которых формируют допустимые
управляющие воздействия, имеют гауссовские функции распределения. В этом случае
можно сформировать генератор управляющих воздействий, оптимальный по критерию
МАВ.
Для составления критерия МАВ сформируем вектор
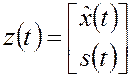 .
.
Тогда математическую модель объекта управления (3.1.1), (3.1.2), (2.1.13)-(2.1.15), (3.1.8)-(3.1.10) можно представить в следующем эквивалентном виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.