|
|
(3.2.1) |
|
|
(3.2.2) |
|
|
(3.2.3) |
При известной оценке возмущающих воздействий ![]() оптимальная по критерию МАВ оценка
оптимальная по критерию МАВ оценка ![]() вектора переменных состояния
вектора переменных состояния ![]() системы управления обращает в максимум
условную плотность
системы управления обращает в максимум
условную плотность ![]() на всем интервале времени
на всем интервале времени ![]() управ-ления, где
управ-ления, где ![]() - множество непрерывных реализаций вектора переменных состояния
- множество непрерывных реализаций вектора переменных состояния ![]() ,
, ![]() - множество непрерывных реали-заций фазовых траекторий (3.2.3) на этом
интервале времени.
- множество непрерывных реали-заций фазовых траекторий (3.2.3) на этом
интервале времени.
Так как вектор ![]() составлен
из случайных гауссовских величин с известными вероятностными характеристиками,
а
составлен
из случайных гауссовских величин с известными вероятностными характеристиками,
а ![]() и
и ![]() - векторы случайных гауссовских процессов, то условная плотность
- векторы случайных гауссовских процессов, то условная плотность ![]() является гауссовской. При этом из (3.2.1)-(3.2.3) следует, что
является гауссовской. При этом из (3.2.1)-(3.2.3) следует, что
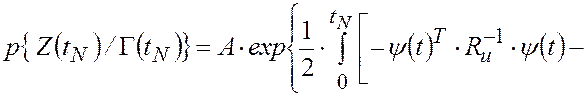
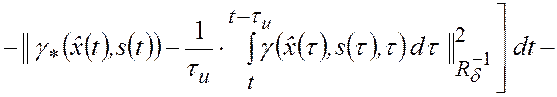
|
|
(3.2.4) |
Таким образом, условная плотность (3.2.4) определяет ПИД-регулятор управляющих воздействий, оптимальный по критерию МАВ.
Критерий обобщенного МНК. Если ввести дополнительную переменную по формулам
|
|
(3.2.5) |
|
|
(3.2.6) |
|
|
(3.2.7) |
то задачу максимизации условной плотности ![]() при ограничении (3.2.1)
можно заменить эквивалентной задачей минимизации функции стоимости
при ограничении (3.2.1)
можно заменить эквивалентной задачей минимизации функции стоимости
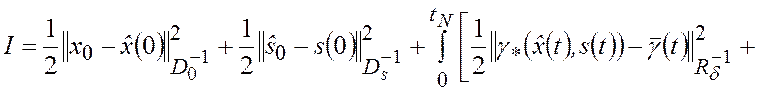
|
|
(3.2.8) |
по переменным ![]() ,
, ![]() и
и ![]() при
ограничениях (3.2.1), (3.2.6), (3.2.7).
при
ограничениях (3.2.1), (3.2.6), (3.2.7).
Очевидно, что если погрешности ![]() и
и ![]() нельзя считать гауссовскими белыми шумами,
то функция стоимости (3.2.8) является функцией стоимости обобщенного МНК, где
нельзя считать гауссовскими белыми шумами,
то функция стоимости (3.2.8) является функцией стоимости обобщенного МНК, где ![]() ,
, ![]() ,
, ![]() и
и ![]() - положительно определенные матрицы весовых коэффициентов.
- положительно определенные матрицы весовых коэффициентов.
3.3. Самонастраивающиеся ПИД-регуляторы
для нелинейных объектов управления
Самонастраивающийся ПИД-регулятор, оптимальный по критерию МАВ. ПИД-регулятор для нелинейного объекта управления (3.2.1)-(3.2.3) с гауссовскими цветными шумами, оптимальный по критерию МАВ (3.2.4), определяет следующая теорема.
Теорема 3. Пусть
объект управления имеет нелинейное уравнение состояния (2.3.1) с начальными
условиями (2.3.2) и на этот объект действуют возмущающие воздействия, изменение
во времени которых описывают с помощью В-сплайнов уравнениями (2.3.3), (2.3.4) с начальными условиями (2.3.5). Пусть вектор
выходных сигналов ![]() измерительных устройств и вектор
переменных состояния
измерительных устройств и вектор
переменных состояния ![]() связаны нелинейным уравнением
(2.3.7), где
связаны нелинейным уравнением
(2.3.7), где ![]() - вектор
средних значений погрешностей измерений,
- вектор
средних значений погрешностей измерений, ![]() - вектор случайных составляющих погрешностей измерений,
которые являются гауссовскими цветными шумами с нулевыми средними значениями и корреляционными
функциями (2.1.22). Пусть
начальные значения
- вектор случайных составляющих погрешностей измерений,
которые являются гауссовскими цветными шумами с нулевыми средними значениями и корреляционными
функциями (2.1.22). Пусть
начальные значения ![]() и
и ![]() являются
гауссовскими случайными величинами, а погрешности аппроксимации
являются
гауссовскими случайными величинами, а погрешности аппроксимации ![]() -
гауссовские цветные шумы с нулевыми средними значениями и корреляционными
функциями (2.1.5). Пусть допустимые
фазовые траектории перехода переменных состояния объекта управления в заданное
конечное состояние заданы уравнением (3.1.6) с погрешностями
-
гауссовские цветные шумы с нулевыми средними значениями и корреляционными
функциями (2.1.5). Пусть допустимые
фазовые траектории перехода переменных состояния объекта управления в заданное
конечное состояние заданы уравнением (3.1.6) с погрешностями ![]() , которые являются гауссовскими случайными
процессами с ковариационными функциями (3.1.6). Пусть допустимые управляющие
воздействия формирует динамическая система (2.1.13)-(2.1.15) из гауссовских белых шумов
, которые являются гауссовскими случайными
процессами с ковариационными функциями (3.1.6). Пусть допустимые управляющие
воздействия формирует динамическая система (2.1.13)-(2.1.15) из гауссовских белых шумов ![]() .
.
Тогда управляющие воздействия ![]() ,
оптимальные по критерию максимума апостериорной вероятности (3.2.4), формирует следующий ПИД-регулятор:
,
оптимальные по критерию максимума апостериорной вероятности (3.2.4), формирует следующий ПИД-регулятор:
|
|
(3.3.1) |
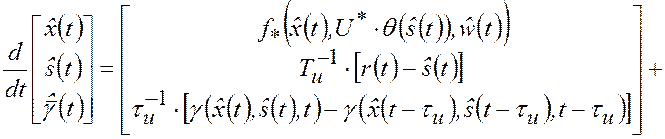
|
|
(3.3.2) |
|
|
(3.3.3) |
с начальными условиями
|
|
(3.3.4) |
где
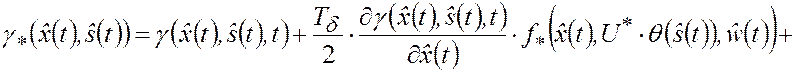
|
|
(3.3.5) |
|
|
(3.3.6) |
|
|
(3.3.7) |
|
|
(3.3.8) |
а ![]() и
и ![]() - оптимальные
по критерию МАВ оценки переменных состояния объекта управления и возмущающих
воздействий соответственно.
- оптимальные
по критерию МАВ оценки переменных состояния объекта управления и возмущающих
воздействий соответственно.
Доказательство.
В рассматриваемую систему управления случайные возмущающие воздействия ![]() ,
, ![]() ,
, ![]() и неизвестные управляющие воздействия
и неизвестные управляющие воздействия ![]() входят линейно. Возмущающие воздействия
входят линейно. Возмущающие воздействия ![]() ,
, ![]() ,
, ![]() являются гауссовскими белыми шумами. Кроме
того, используется квадратичный критерий оптимальности управления (3.2.8).
Поэтому можно применять теорему разделения [20], [29].
являются гауссовскими белыми шумами. Кроме
того, используется квадратичный критерий оптимальности управления (3.2.8).
Поэтому можно применять теорему разделения [20], [29].
Случайные возмущающие воздействия ![]() и
погрешности измерений
и
погрешности измерений ![]() являются гауссовскими белыми
шумами. Поэтому, как это было доказано в разделе 2.3, оптимальные по критерию
МАВ оценки
являются гауссовскими белыми
шумами. Поэтому, как это было доказано в разделе 2.3, оптимальные по критерию
МАВ оценки ![]() и
и ![]() переменных состояния объекта управления
переменных состояния объекта управления ![]() и возмущающих воздействий
и возмущающих воздействий ![]() формирует ПИД-наблюдатель (2.3.24)-(2.3.27).
формирует ПИД-наблюдатель (2.3.24)-(2.3.27).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.