Синтез самонастраивающихся регуляторов нелинейных систем автоматического управления, страница 5

Из (3.4.15) и (3.4.16)  следует, что матрицы  и  положительно полуопределенные, поэтому решение уравнения Риккати (3.4.13) асимптотически устойчиво при любых погрешностях задания начальных условий [21].

Разработанная адаптивная система автоматического управления объектом с неизвестным математическим описанием происходящих в нем процессов, в отличие от известного самоорганизующегося регулятора Красовского [9], реализует алгоритм ПИ-регулирования. ПИ-регулятор (3.4.21)-(3.4.26), (3.4.12)-(3.4.17) использует текущие значения погрешностей управления  и оценки их средних значений , вычисленные в скользящем временном окне. За счет этого уменьшается (либо полностью устраняется) статическая погрешность управления.

Кроме того, в отличие от регулятора Красовского, в разработанной системе управления при вычислении параметров настройки ПИ-регулятора, объединенных в матрицы  и , используют результаты измерений выходных сигналов объекта управления и реализованные значения управляющих воздействий. Регулятор Красовского такую информацию не использует, а адаптацию системы управления обеспечивает выбором в каждом временном окне (цикле управления) наилучшей модели из множества используемых альтернативных моделей объекта управления (путем перебора всех вариантов).

3.4.2. Сравнительный анализ эффективности алгоритмов управления

Для анализа эффективности разработанных алгоритмов управ-ления было выполнено имитационное моделирование процессов функционирования трех альтернативных систем управления одинако-выми объектами, на которые действует одно и то же возмущающее воздействие. В первой (эталонной) системе управления математичес-кая модель объекта управления известна и известно оптимальное управляющее воздействие . Результаты измерений выходного сигнала этого объекта используют в системах управления двумя другими объектами в качестве задания для формирования управляющих воздействий с помощью самоорганизующегося П‑регулятора [9] и адаптивного ПИ‑регулятора (3.4.12)-(3.4.26). При этом предполагается, что математические модели этих двух объектов управления неизвестны.

Все три объекта управления имеют нелинейное уравнение состояния

с начальными условиями

где  – переменная состояния объекта управления;  – постоянная времени объекта управления;  – коэффициент уси-ления управляющего воздействия;  – управляющее воздействие;  – возмущающее воздействие, которое является случайным стационарным процессом с нулевым средним значением и ковариационной функцией , приведенной на рисунке 3.2.

На каждый объект управления действует своя реализация  возмущающего воздействия .

Выходной сигнал  измерительного устройства эталонной системы управления связан с переменной состояния объекта управления  уравнением наблюдения

где  – случайная погрешность измерений, которая имеет нулевое среднее значение и ковариационную функцию , изображенную на рисунке 3.3.

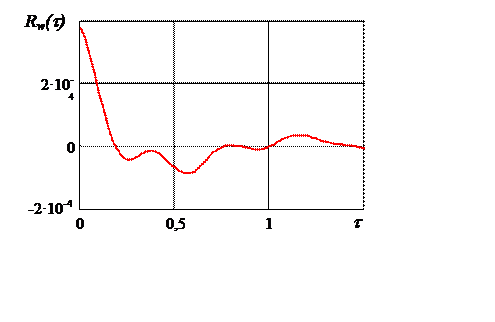
Рис. 3.2. Ковариационная функция возмущающего воздействия

Выходные сигналы  и  измерительных устройств других объектов управления связаны с переменной состояния своего объекта этим же уравнением наблюдения. В каждом измерительном устройстве в качестве погрешности измерений используется своя реализация случайного процесса .

График изменения во времени управляющего воздействия , формируемого эталонной системой управления, приведен на рисунке 3.4.

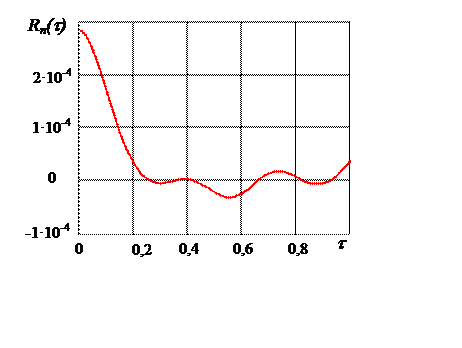
Рис. 3.3. Ковариационная функция погрешностей измерений

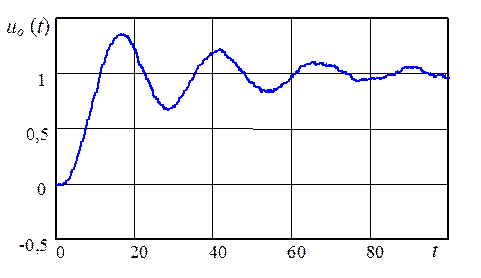
Рис. 3.4. График изменения управляющего воздействия, формируемого эталонной системой управления

График изменения во времени выходного сигнала  измерительного устройства эталонной системы управления приведен на рисунке 3.5.

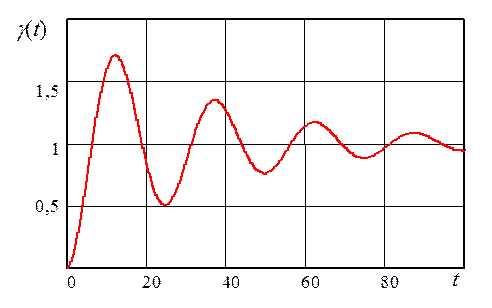
Рис. 3.5. График изменения во времени выходного сигнала измерительного устройства эталонной системы управления

Результаты моделирования процедур управления этим объектом с помощью самонастраивающегося П-регулятора и адаптивного ПИ-регулятора (3.4.12)-(3.4.26) приведены на рисунках 3.6–3.9.