Синтез самонастраивающихся регуляторов нелинейных систем автоматического управления, страница 7

В соответствии с методом невязки оптимальное значение параметра регуляризации следует определять путем решения уравнения

где  - оптимальная оценка переменной состояния объекта управления, вычисленная по математической модели, которая является функцией параметра регуляризации;  - допустимая погрешность управления.

 Оценку параметра регуляризации, оптимальную по критерию (3.5.21), можно осуществить с помощью алгоритма идентификации MTI [5]:

с начальным условием

где  - число, характеризующее скорость адаптации.

Таким образом, максимальное по быстродействию управление линейным объектом (3.5.1) с ограничениями (3.5.2)–(3.5.9) осущест-вляет адаптивная система автоматического управления, состоящая из измерительного устройства (3.5.3), (3.5.4) и самонастраивающегося ПИД-регулятора (3.5.12)–(3.5.23).

Результаты имитационного моделирования. Исследование адаптивной системы автоматического управления (3.5.12)–(3.5.23) выполнено имитационным моделированием.

Исследовалась система управления объектом (3.5.1), который  имеет следующие параметры:

На объект управления действует неконтролируемое возмущаю-щее воздействие

где , , ,  - постоянные параметры, случайным образом выбираемые из диапазонов их возможных значений:

 - случайный процесс с нулевым средним значением и дисперсией .

На рисунке 3.10 приведена одна реализация возмущающего воздействия .

Управление осуществлялось с помощью адаптивной системы управления (3.5.12)–(3.5.23) и ПИД-регулятора с параметрами настройки, определенными по методу нейроуправления [18], при действии на объект возмущающего воздействия (3.5.25).

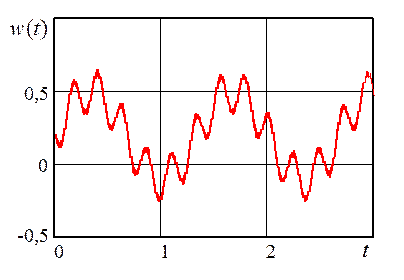
Рис. 3.10. Реализация возмущающего воздействия  

при ; ;  и

Моделированием на ЭВМ было сформировано 100 различных реализаций возмущающего воздействия при значениях параметров, выбираемых случайным образом из диапазонов их значений, определенных ограничениями (3.5.26). Было установлено, что обе системы управления обеспечивают во всех рассмотренных случаях статическую погрешность управления  с примерно одинаковыми среднеквадратическими отклонениями. При этом ПИД-регулятор с настройкой параметров по методу нейроуправления обеспечивает среднеквадратическое отклонение , а разработанный алгоритм - .

Результаты управления для случая, когда на объект управления действует возмущение, изображенное на рисунке 3.10, приведены на рисунках 3.11-3.13.

На рисунке 3.11 приведен график (кривая 1) изменения оптимального управляющего воздействия:

с помощью которого рассматриваемый объект управления переводят из начального состояния в конечное состояние за минимальное время при отсутствии возмущающего воздействия. График изменения выходного сигнала объекта управления, соответствующий этому случаю управления, приведен на рисунке 3.12 (кривая 1).

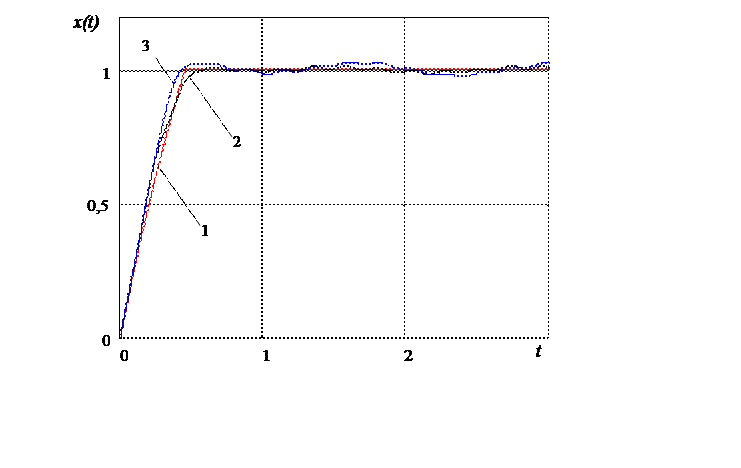
Рис. 3.11. Графики изменения во времени выходного сигнала объекта управления: 1 - при управляющем воздействии (3.5.27); 2 - при управляющем воздействии, сформированном по алгоритму (3.5.12) - (3.5.23); 3 - при управляющем воздействии, сформированном по алгоритму нейроуправления

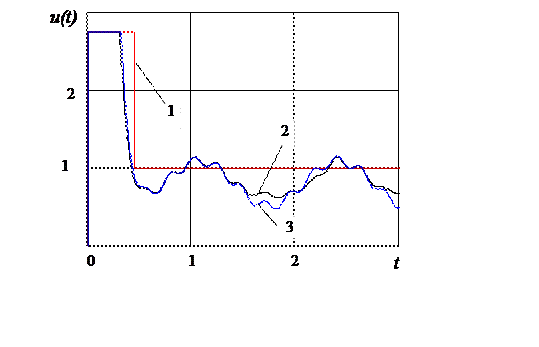
Рис. 3.12. Графики изменения во времени управляющих воздействий:

1 - управляющее воздействие (3.5.27); 2 - управляющее воздействие, сформированное по алгоритму (3.5.12)-(3.5.23); 3 - управляющее воздействие, сформированное по алгоритму нейроуправления

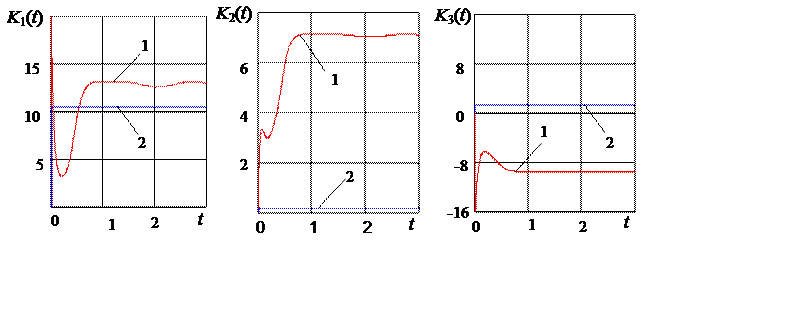
Рис. 3.13. Графики изменения во времени параметров настройки регуляторов

Таким образом, результаты моделирования показали, что разработанная адаптивная система автоматического управления и ПИД-регулятор с настройкой параметров по методу нейроуправления обеспечивают управление линейным объектом (3.5.1) при действии возмущающего воздействия (3.5.25), близкое к оптимальному управлению этим объектом при отсутствии возмущений. Однако разработанная адаптивная система автоматического управления не нуждается в специальном режиме настройки параметров и может применяться для оптимального управления нелинейными объектами.