Синтез самонастраивающихся регуляторов нелинейных систем автоматического управления, страница 4

3.4. Адаптивный ПИ-регулятор для объекта

с неизвестной математической моделью

3.4.1. Вывод алгоритма управления

Постановка задачи. Рассматривается задача синтеза  адаптивной системы управления объектом, в котором происходят процессы с неизвестным математическим описанием.

В разделе 2.4 разработан ПИ-наблюдатель переменных состояния такого объекта в виде динамической системы, состояние которой описывают уравнениями (2.4.19)–(2.4.25), (2.4.15)-(2.4.17).

Предполагается, что во временном окне с номером  (), которое имеет длительность , множество допустимых управляющих воздействий задано неравенствами

, , .

(3.4.1)

Это множество допустимых управляющих воздействий можно задать следующими уравнениями:

,

(3.4.2)

(3.4.3)

с начальными условиями

,  ,

(3.4.4)

где  - случайный процесс, реализации которого принимают значения в интервале [-1, 1].

Кроме того, известно, что выходной сигнал объекта управления  должен изменяться во времени так, чтобы выполнялось условие

,

(3.4.5)

где  – заданная функция;

;

(3.4.6)

 – среднее значение погрешности управления:

;

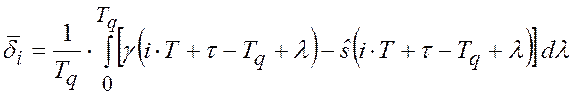 – допустимая погрешность управления, которая является случайным процессом с нулевым средним и дисперсий .

Предполагается, что ограничения в виде неравенств, если они имеются, включены в условие (3.4.5) с помощью преобразования (3.1.5).

Требуется определить управляющие воздействия , обращающие в минимум функцию стоимости обобщенного МНК

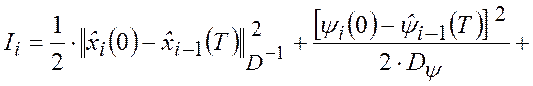
(3.4.7)

при ограничениях (2.4.19)-(2.4.25), (3.4.6).

Такие управляющие воздействия формирует ПИ-регулятор (3.3.1)-(3.3.8). Однако для рассматриваемой задачи уравнения (3.3.1)-(3.3.8) можно существенно упростить, так как в этом случае можно воспользоваться оценкой среднего значения погрешности управления, вычисленной усреднением по времени в скользящем временном окне по формуле

.

(3.4.8)

Для решения задачи синтеза системы управления уравнение (2.4.19) с учетом (3.4.2) запишем в следующем виде:

,

(3.4.9)

.

(3.4.10)

Тогда синтез регулятора управляющих воздействий следует выполнять минимизацией функции стоимости (3.4.7) по переменным ,  и  при ограничениях (3.4.2), (3.4.3), (3.4.6), (3.4.8)-(3.4.10).

Алгоритм управления. В разделе 3.3 было показано, что эту задачу с помощью метода множителей Лагранжа и инвариантного погружения возникающей двухточечной краевой задачи можно преобразовать в задачу Коши для системы уравнений (3.3.1)-(3.3.8). В рассматриваемом случае эти уравнения принимают следующий вид:

,

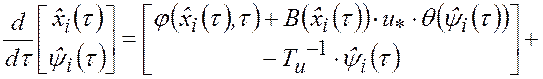
(3.4.11)

,

(3.4.12)

,

(3.4.13)

; ,

(3.4.14)

, ,

(3.4.15)

,  ,

(3.4.16)

.

(3.4.17)

Из (3.4.5), (3.4.6) и (2.4.6) видно, что погрешность управления

,  ,

(3.4.18)

где  – выходной сигнал измерительного устройства.

Из (3.4.8) следует, что , где  - решение дифференциального уравнения

, ,

(3.4.19)

с начальным  условием

.

(3.4.20)

Из уравнений (2.4.18), (2.4.19), (3.4.2), (3.4.10) и (3.4.11) следует, что оптимальные управляющие воздействия  необходимо формировать по алгоритму

,  ,

(3.4.21)

,

(3.4.22)

,

(3.4.23)

(3.4.24)

с начальными  условиями

,  ,   .

(3.4.25)

Для гарантированного выполнения ограничения (3.4.1) этот алгоритм следует дополнить еще одним уравнением:

(3.4.26)

Таким образом, уравнения (3.4.21)-(3.4.26) совместно с уравнениями (3.4.12)-(3.4.17), (2.4.19)-(2.4.25) и (2.4.15)-(2.4.17) определяют адаптивную систему автоматического управления объектом, в котором происходят процессы с неизвестным математическим описанием.

Управляющие воздействия, формируемые ПИ-регулятором (3.4.21)-(3.4.26), (3.4.12)-(3.4.17), (2.4.19)-(2.4.25), (2.4.15)-(2.4.17), обеспечивают минимальные выборочные оценки дисперсии погрешности управления (средний по времени квадрат отклонения погрешности управления  (3.4.18) от своего среднего значения , вычисленного усреднением по времени в скользящем временном окне по формуле (3.4.8)).