Синтез самонастраивающихся регуляторов нелинейных систем автоматического управления, страница 6

Из рисунков 3.6 и 3.7 видно, что в рассматриваемой задаче       П-регулятор формирует управляющее воздействие в виде физически нереализуемой последовательности импульсов, следующих друг за другом с высокой частотой. Этот регулятор формирует переменную состояния объекта управления в виде случайного процесса. Установка на выходе регулятора сглаживающего фильтра приводит к появлению статической погрешности управления.

Адаптивный ПИ-регулятор (3.4.12)-(3.4.26) формирует управ-ляющее воздействие в виде непрерывного сигнала, плавно изменяю-щегося с течением времени (рис. 3.8).

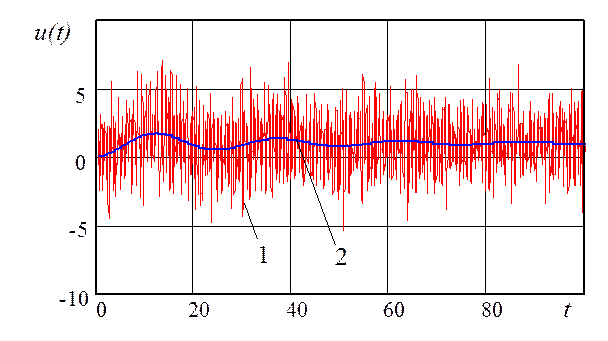
Рис. 3.6. Управляющее воздействие, формируемое П-регулятором:

 1 – управляющее воздействие, формируемое П-регулятором; 2 – управляющее воздействие, формируемое эталонной системой управления

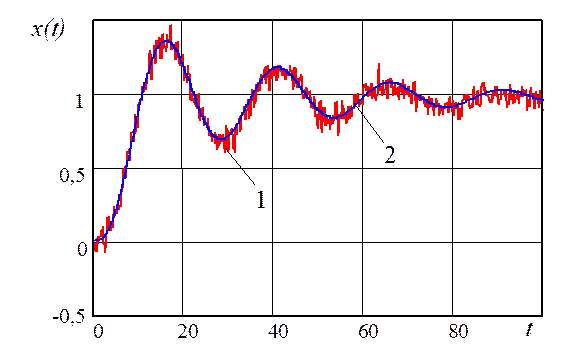
Рис. 3.7. Результаты управления с помощью П-регулятора:

1 – переменная состояния объекта управления с П-регулятором;

2 – переменная состояния объекта управления эталонной системы

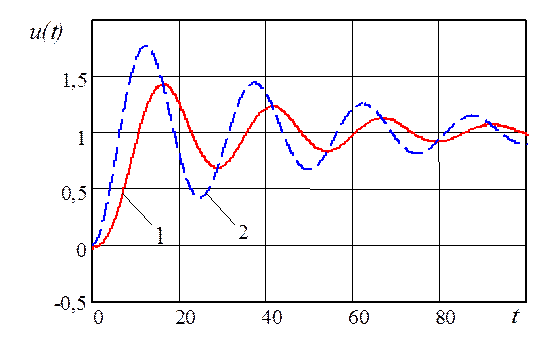
Рис. 3.8. Управляющие воздействия, формируемые ПИ‑регулято-

ром (3.4.12)-(3.4.26) (линия 1) и эталонной системой управления (линия 2)

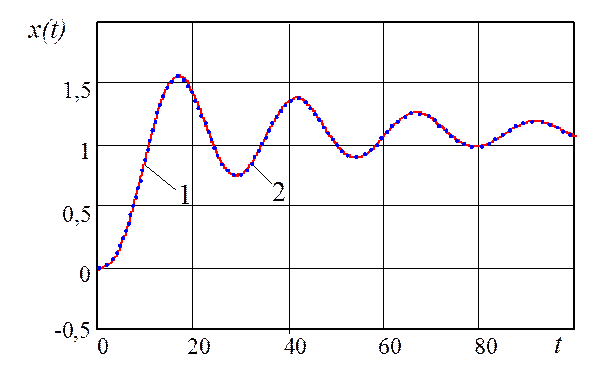
Рис. 3.9. Результаты управления с помощью ПИ-регулятора:

1 – переменная состояния объекта с ПИ-регулятором (3.4.12)-(3.4.26);

2 – переменная состояния объекта управления эталонной системы

Регулятор (3.4.12)-(3.4.26) формирует переменную состояния объекта управления в виде сигнала, медленно изменяющегося с течением времени (рис. 3.9). При этом он обеспечивает относитель-ную погрешность управления не превышающую .

Таким образом, результаты моделирования показали, что адаптивная система автоматического управления с ПИ‑регулятором (3.4.12)-(3.4.26) обеспечивают управление объектом с неизвестной математической моделью, близкое к оптимальному управлению этим объектом с известной математической моделью.

3.5. Сравнительный анализ алгоритмов управления линейным объектом

Постановка задачи. Рассматривается задача о наискорейшем переводе линейного объекта из начального состояния в заданное новое состояние и удержании его в этом состоянии. Объект управления имеет уравнение состояния

(3.5.1)

с начальными условиями

;   ,

(3.5.2)

и неизвестным возмущающим воздействием .

Выходной сигнал  измерительного устройства связан с переменной состояния объекта управления  уравнением наблюдения

,

(3.5.3)

где  – погрешность математической модели измерительного устройства, которую в скользящем временном окне длительностью  можно представить следующим образом:

,

(3.5.4)

где  – случайный процесс с нулевым средним значением и дисперсией .

Требуется с помощью ограниченного управляющего воздействия  за минимальное время  перевести объект управления из начального состояния (3.5.2) в режим функционирования, в котором

; ,

(3.5.5)

где  – погрешность управления.

Погрешность управления имеет математическое ожидание, оценку которого можно вычислить усреднением по времени в скользящем временном окне по формуле

,

(3.5.6)

и  дисперсию  случайной составляющей .

Множество допустимых управляющих воздействий  задано следующими уравнениями:

;

(3.5.7)

,

(3.5.8)

с начальными условиями

;   .

(3.5.9)

В скользящем временном окне длительностью  определим показатель оптимальности управления

,

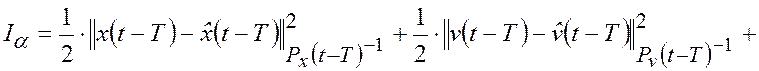
(3.5.10)

где  -  параметр регуляризации, оптимальное значение которого следует определить в процессе управления;

;   ;   ;  .

(3.5.11)

Алгоритм управления. Из формул (3.5.1)–(3.5.11) следует, что алгоритм управления (3.3.1)-(3.3.8) в рассматриваемой задаче принимает следующий вид:

,

(3.5.12)

,

(3.2.13)

,

(3.5.14)

,

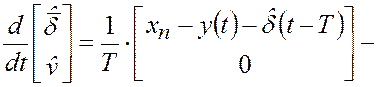
(3.5.15)

,

(3.5.16)

,

(3.5.17)

,    ,  ,

(3.5.18)

,  ,

(3.5.19)

,  .

(3.5.20)

Алгоритм идентификации параметра регуляризации. Для оценивания параметра регуляризации можно использовать преоб-разование математической модели объекта, описанное в разделе 2.4. Кроме того, можно применять метод невязки [55] и алгоритм MTI (Массачусетского технологического института) [5].