Решение задач № 1-30 по дисциплине "Организация производства" (Расчет средних и относительных показателей вариации. Определение величины среднего сбора картофеля одним работником по всем бригадам)

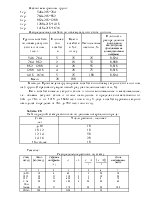
Задача1: имеются  данные  по  группе предприятий:

    Рассчитать средние и относительные показатели вариации.

Решение:

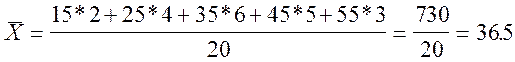
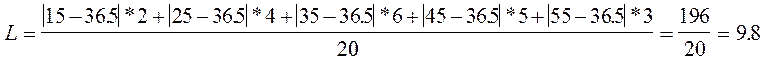
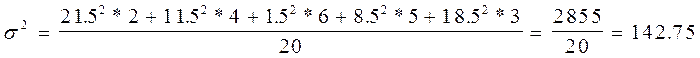
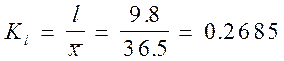
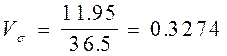
Задача 2

Имеются данные о количестве участков  в  цехах  предприятия:

Число участков   1      2      3      4      5       6  и более

в цехе

Число цехов        1      3      5      3      2       2

Рассчитать величину дисперсии одним из существующих способов.

Решение:

                        1*1+2*3+3*5+4*3+5*2+6*2      56

               x  =                   16                          =     16    =  3.5

Дисперсия:

                  s² = x² - x²= 14.25-3.5²=2

                          1*1+4*3+9*5+16*3+25*2+36*2                    228

                 X ²=                   16                                       =    14   = 14.25

Задача 3

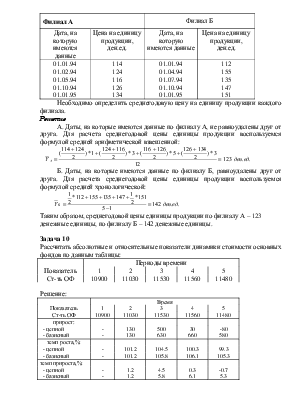
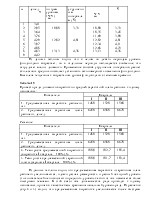
Рассчитать абсолютные и средние показатели вариации на основе имеющихся данных:

Решение:

Расчет показателей вариации

Абсолютные показатели вариации:

-  размах вариации:  R = 22-6 =16  (лет)

-  среднее значение признака 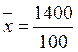 = 14 (лет)

-  среднее линейное отклонение: 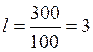(года)

-  дисперсия: σ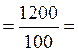² 12

-  среднее квадратическое отклонение: σ 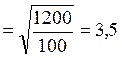(года)

Задача 4

Провели исследование 20 из 100 единиц совокупности по фондовооруженности труда. Имеются следующие данные: средняя фондовооруженность труда равна 22 ден.ед., дисперсия фондовооруженности труда - 55 ден. ед. Отбор случайный, бесповторный, вероятность равна 0,954. Определить среднюю и предельную ошибки выборки по фондовооруженности труда для предприятий,  а также пределы для генеральной средней.

Решение:

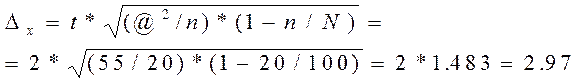
                           22-2.97<= x <=22+2.97

                              19<= x <=25  

Задача 5

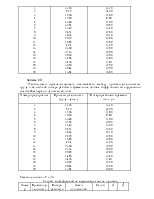
Провели исследование 20 из 100 предприятий по производительности труда. Имеются следующие данные: средняя производительность труда равна ден.ед., дисперсия производительности труда -  ден. ед. Отбор случайный, бесповторный, вероятность равна 0,954. Определить среднюю и предельную ошибки выборки по производительность труда, пределы для генеральной средней, а также относительную ошибку выборки.

Решение:

Средняя ошибка выборки будет равна: 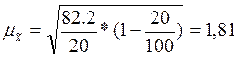( ден. ед.).

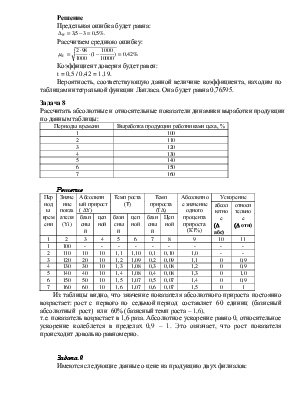
Отсюда получим величину предельной ошибки (t=2):

( ден. ед.).

Вычислим пределы для генеральной средней: .

На основе проведенной выборки сделаем вывод: установлена средняя производительность труда для предприятий с возможным отклонением в ту или иную сторону не более, чем на 3,63 ден.ед., или в пределах от 17,88 до 25,14 ден.ед., что можно утверждать с вероятностью 0,954, т.е. в 954 случаях из 1000.

отн. = 3,63/21,51=0,169 или 16,9%,

Следовательно, для оценки средней выборка репрезентативна.

Задача 6

 Исследована группа  из 20 предприятий (из 100) по величине производительности труда. Предприятий с низким уровнем производительности оказалось 2. С вероятностью 0,683 необходимо найти пределы, в которых можно ожидать долю предприятий со средним  и высоким уровнем производительности, а также относительную ошибку выборки. Выборка случайная, бесповторная.

Решение

Имеются данные: n=20 (шт.), N=100 (шт.), m=20-2=18 (шт.), t=1, P(t)=0,683, w=18/20=0,9.

Определим среднюю ошибку выборки:

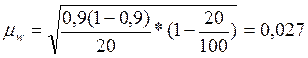 или 2,7%

Рассчитаем предельную ошибку:

Определим пределы, в которых можно ожидать долю предприятий с высоким и средним уровнем производительности:

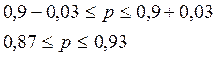
С вероятностью 0,683, т.е. в 683 случаях из 1000, можно утверждать, что средний процент предприятий с высоким и средним уровнем производительности будет находиться в пределах от 87 до 93%.

 отн.= 0,03/0,9=0,033 или 3,3%

Следовательно, для оценки доли выборка репрезентативна.