|
№ предприятия |
Базисный период |
Отчётный период |
||
|
Произведено изделий, шт. |
Цена единицы изделия, ден.ед. |
Произведено, изделий, шт. |
Цена единицы изделия, ден.ед. |
|
|
q0 |
p0 |
q1 |
p1 |
|
|
1 2 |
2000 3000 |
5,5 6,5 |
1900 3200 |
5,8 6,1 |
Необходимо определить общие (агрегатные) индексы цены, физического объема и стоимости продукции. Объяснить их смысл.
Решение
Рассчитаем агрегатный индекс цены по формуле Пааше:
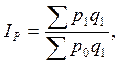
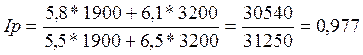 или
97,7%.
или
97,7%.
Абсолютное изменение стоимости за счет изменения цены
равно: ![]() :
:
![]() .
.
Рассчитаем агрегатный индекс физического объема
продукции по формуле 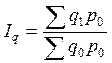 :
:
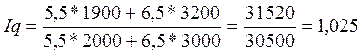 или
102,5%.
или
102,5%.
Абсолютное изменение стоимости за счет изменения
физического объема продукции равно: ![]() :
:
![]() .
.
Рассчитаем агрегатный индекс стоимостного объема продукции по
формуле: 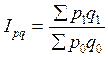 :
:
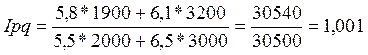 или
100,1%
или
100,1%
Абсолютное изменение стоимости за счет изменения цен
и физического объема продукции равно: ![]() :
:
![]() .
.
Между абсолютными изменениями стоимости имеется следующая взаимосвязь: 40 = 750 – 710.
Между индексами существует следующая взаимосвязь: Ipq = Ip * Iq .
1,001 = 1,025 * 0,977 .
Исходя из произведенных расчетов, можно сделать следующие выводы: общая цена изделия по двум предприятиям снизилась в отчетном периоде по сравнению с базисным на 2,3 %, физический объем продукции возрос на 2,5%, стоимость продукции увеличилась на 0,1%. Стоимость продукции по двум предприятиям возросла на 40 ден. единиц, в том числе за счет изменения цены произошло снижение на 710 ден. единиц, а за счет изменения физического объема стоимость продукции увеличилась на 750 денежных единиц.
Задача 19
По данным таблицы необходимо рассчитать средний арифметический индекс физического объема продукции, тождественный агрегатному.
|
№ предприятия |
Базисный период |
Отчётный период |
||
|
Произведено изделий, шт. |
Цена единицы изделия, ден.ед. |
Произведено, изделий, шт. |
Цена единицы изделия, ден.ед. |
|
|
q0 |
p0 |
q1 |
p1 |
|
|
1 2 |
2000 3000 |
5,5 6,5 |
1900 3200 |
5,8 6,1 |
Решение
Для этого рассчитаем индивидуальные индексы физического объема продукции по двум предприятиям:
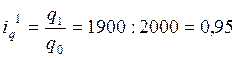
![]()
Средний арифметический индекс физического объема продукции, тождественный агрегатному, будет иметь вид:
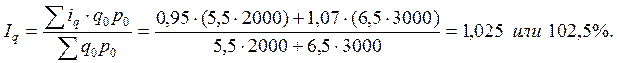
Аналогичная величина получилась и при расчете индекса физического объема продукции по агрегатной формуле. Таким образом, можно сделать вывод о тождественности двух индексов.
Задача 20
Необходимо рассчитать индексы средней цены продукции двух предприятий переменного состава, постоянного состава и структурных сдвигов по данным таблицы.
|
№ предприятия |
1 период |
2 период |
||
|
произведено, шт. |
цена единицы изделия, ден.ед |
произведено, шт. |
цена единицы изделия, ден.ед |
|
|
1 2 |
1219 1100 |
4,40 4,10 |
1888 1500 |
4,00 4,00 |
Рассчитаем индексы постоянного, переменного состава и структурных сдвигов средней цены продукции по двум предприятиям. Индекс переменного состава равен:
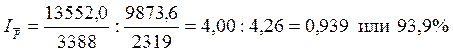
![]()
|
№ предприятия |
1 период |
2 период |
Объем продукции в стоимостном выражении в 1-м периоде |
Объем продукции в стоимостном выражении во 2-м периоде |
Объем продукции 2-го периода в ценах 1-го периода |
||
|
произведено, шт. |
цена единицы изделия, ден.ед |
произведено, шт. |
цена единицы изделия, ден.ед |
||||
|
i |
q0 |
p0 |
q1 |
p1 |
p0q0 |
p1q1 |
p0q1 |
|
1 2 |
1219 1100 |
4,40 4,10 |
1888 1500 |
4,00 4,00 |
5363,60 4510,00 |
7552,00 6000,00 |
8307,20 6150,00 |
|
2319 |
* |
3388 |
* |
9873,60 |
13552,00 |
14457,20 |
|
Таким образом, средняя цена продукции в целом по двум предприятиям составила в отчетном периоде 4,00 денежные единицы, в базисном - 4,26 денежных единиц, т.е. снизилась на 0,26 денежных единиц или на 6,1%. На изменение средней цены продукции оказали влияние два фактора:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.