Решение задач № 1-30 по дисциплине "Организация производства" (Расчет средних и относительных показателей вариации. Определение величины среднего сбора картофеля одним работником по всем бригадам), страница 2

Задача 7

В выборке объемом 1000 единиц доля бракованных изделий составила 3%. Выборка случайная, бесповторная. Необходимо определить вероятность того, что во всей партии изделий (10000 штук) доля бракованных изделий будет находиться в пределах от 2,5 до 3,5%.

Решение

Предельная ошибка будет равна:

Рассчитаем среднюю ошибку:

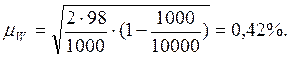
Коэффициент доверия будет равен:

t = 0,5 / 0,42 = 1,19.

Вероятность, соответствующую данной величине коэффициента, находим по таблицам интегральной функции Лапласа. Она будет равна 0,76595.

Задача 8

Рассчитать абсолютные и относительные показатели динамики выработки продукции по данным таблицы:

Решение

Из таблицы видно, что значение показателя абсолютного прироста постоянно возрастает: рост с  первого по  седьмой период  составляет  60  единиц  (базисный  абсолютный  рост)  или  60% (базисный темп роста – 1,6),

т.е. показатель возрастает в 1,6 раза. Абсолютное ускорение равно 0, относительное ускорение колеблется в пределах 0,9 – 1. Это означает, что рост показателя происходит довольно равномерно.

Задача 9.

Имеются следующие данные о цене на продукцию двух филиалов:

Необходимо определить среднегодовую цену на единицу продукции каждого филиала.

Решение

А. Даты, на которые имеются данные по филиалу А, не равноудалены друг от друга. Для расчета среднегодовой цены единицы продукции воспользуемся формулой средней арифметической взвешенной:

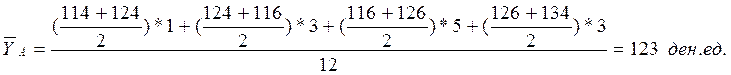
Б. Даты, на которые имеются данные по филиалу Б, равноудалены друг от друга. Для расчета среднегодовой цены единицы продукции воспользуемся формулой средней хронологической:

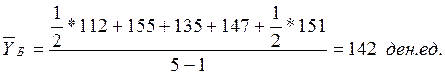
Таким образом, среднегодовой цены единицы продукции по филиалу А – 123 денежные единицы, по филиалу Б – 142 денежные единицы.

Задача 10

Рассчитать абсолютные и относительные показатели динамики стоимости основных фондов по данным таблицы: