Решение задач № 1-30 по дисциплине "Организация производства" (Расчет средних и относительных показателей вариации. Определение величины среднего сбора картофеля одним работником по всем бригадам), страница 8

Рис.2. Графическое представление медианы на кумуляте распределения.

Задача 25

Необходимо определить общие индексы физического объема потребления товаров и услуг всем населением, а также в расчете на душу населения, исходя из данных о расходах населения республики при условии, что средняя годовая численность населения в базисном периоде равна 10265 тыс. человек, а в отчетном - 10236 тыс. человек.

Решение

Преобразуем формулы по средней геометрической взвешенной и получим:

;

.

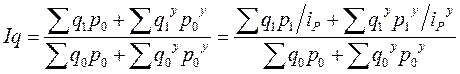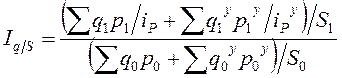          Таким образом:

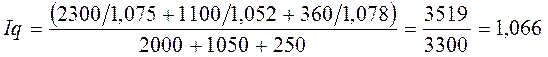  или 106,6% ;

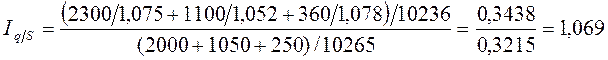  или 106,9 %.

Объем потребления всем населением материальных благ и услуг во втором периоде по сравнению с первым возрос на 6,6%. Объем потребления материальных благ и услуг на душу населения во втором периоде по сравнению с первым возрос на 6,9% за счет некоторого изменения численности населения.

Задача 26

Численность наличного населения области на начало года составила 920 тыс. чел., в том числе 5 тыс. чел. временно проживающих. Из числа постоянного населения области на начало года отсутствовало 7 тыс. чел. На конец года в области оказалось 940 тыс. чел. из числа постоянного населения  и 2 тыс. чел. временно проживающих. Из числа постоянного населения временно отсутствовало 6 тыс. чел.

Необходимо определить:

1.  Численность постоянного населения на начало года.

2. Численность наличного населения на конец года.

3. Прирост постоянного и наличного населения за год.

4. Среднегодовую численность наличного населения.

Решение:

1. Численность постоянного населения на начало года будет равна:

Sпн _н.г.= Sнн_н.г. – Sвп_н.г. + Sво_н.г. = 920 – 5 + 7 = 922 (тыс.человек).

2. Численность наличного населения на конец года рассчитаем, как:

Sнн _к.г.= Sпн_к.г.– Sво_к.г + Sвп_к.г= 940 – 6 + 2 = 936 (тыс.человек).

3. Найдем абсолютный прирост численности населения за год:

а) Dпн = Sпн_к.г. – Sпн_н.г. = 940 – 922 = 18 (тыс.человек).

б) Dнн = Sнн_к.г. - Sнн_н.г. = 936 – 920 = 16 (тыс.человек).

4. Среднегодовую численность наличного населения находим по формуле средней арифметической простой:

Таким образом, на начало года численность постоянного населения составила 922 тысяч человек. На конец года численность наличного населения оказалась равной 936 тысяч человек. Прирост за год постоянного населения составил 18 тысяч человек, наличного - 16 тысяч человек. Величина среднегодовой численности наличного населения равна 928 тысяч человек.

Задача 27

Численность детей города на 1 сентября 1998 года в возрасте от 4-х до 7-ми лет и вероятность их дожития представлены в таблице 7.8. Необходимо определить возможный контингент учащихся начальных классов (от 6-ти до 9-ти лет) на 1 сентября 2000 года.

Рассчитаем возможный контингент учащихся:

а) 1-го класса: 9000*0,99853*0,99985 = 8985 (человек);

б) 2-го класса: 8900*0,99985*0,99895 = 8889 (человек);

в) 3-го класса: 8750*0,99895*0,99909 = 8733 (человек);

г) 4-го класса: 8700*0,99909*0,99925 = 8686 (человек).

Таким образом, в 2000 году в 1-4 классах, вероятно, смогут учиться 35293 ребенка.