Решение задач № 1-30 по дисциплине "Организация производства" (Расчет средних и относительных показателей вариации. Определение величины среднего сбора картофеля одним работником по всем бригадам), страница 4

Из данных таблицы видно, что в целом по девяти периодам уровень фондоотдачи возрастает, но в отдельные периоды наблюдается снижение, что затрудняет анализ динамики. Применение способа укрупнения интервалов, расчет скользящих средних позволяет установить закономерность изменения фондоотдачи. Выявлена тенденция к возрастанию уровня фондоотдачи с течением времени.

Задача 15

Привести ряды динамики выработки и средней заработной платы рабочих к одному основанию:

Решение:

Из данных таблицы видно, что среднемесячная выработка и заработная плата рабочего увеличиваются, однако разная размерность и разный исходный уровень этих показателей не позволяют определить, уровень какого из них изменяется более быстрыми темпами. В этой связи оба динамических ряда приводят к одному основанию, приняв в качестве базы сравнения начальный уровень ряда. Из расчетов (стр.3 и 4) видно, что среднемесячная выработка увеличивается более быстрым темпом, чем среднемесячная заработная плата.

Задача 16

Произвести аналитическое выравнивание средней выработки за ряд периодов по прямой линии:

Решение:

          Рассчитаем параметры уравнения тренда:

;  .

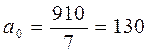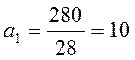Таким образом, уравнение тренда будет иметь вид:

Yt = 130+10t.

Если t увеличивается на 1, то средняя выработка возрастает на 10%.

Задача 17

При административно-территориальных изменениях (при изменении границ предприятия) получены следующие данные по объему производства:

Необходимо провести смыкание рядов динамики.

Решение

Коэффициент соотношения двух уровней равен:

К = 650/450=1.44

Рассчитаем объем производства в новых границах в первом периоде:

420*1.44=604.8

Сопоставимый ряд в новых границах будет иметь вид:

Задача 18

По двум предприятиям имеются данные по одному виду продукции: