Также
можно определить поверхностные силы на грани по оси ![]() .
.
Рассмотрим равновесие параллелепипеда, находящегося в движущейся жидкости, используя принцип Даламбера.
Согласно
принципу Даламбера уравнение движения можно рассматривать как уравнение
равновесия, если ввести силы инерции. Полагаем, что параллелепипед массой ![]() перемещается со
скоростью
перемещается со
скоростью ![]() , составляющие
этой скорости
, составляющие
этой скорости ![]() ,
, ![]() ,
, ![]() .
.
Сила
инерции 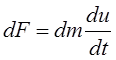 (
(![]() - ускорение).
- ускорение).
Проекции силы инерции на соответствующие координатные оси:
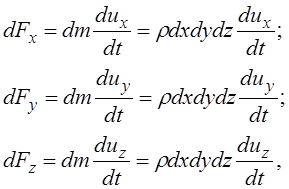 (3.57)
(3.57)
где ![]() ,
, ![]() ,
, ![]() -
проекции ускорении на оси
-
проекции ускорении на оси ![]() ,
, ![]() ,
, ![]() .
.
Составим
уравнение равновесия для сил, действующих на рассматриваемый параллелепипед
жидкости, с учетом силы инерции по осям ![]() и
и ![]() :
:
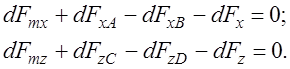 (3.58)
(3.58)
Подставляя в (3.58) полученные ранее зависимости (3.53), (3.55), (3.56) и (3.57), получим следующие уравнения
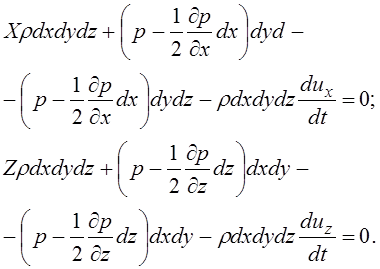
Раскрыв
скобки и разделив полученные выше уравнения на ![]() , напишем
, напишем
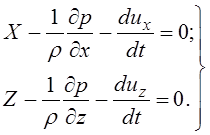 (3.59)
(3.59)
Аналогично можно получить уравнение по оси у:
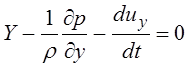 (3.60)
(3.60)
Уравнения (3.59) и (3.60) можно записать в виде системы уравнений:
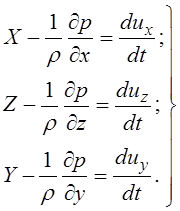 (3.61)
(3.61)
В общем
случае величины ![]() ,
, ![]() ,
, ![]() являются функцией координат
являются функцией координат ![]() ,
, ![]() ,
, ![]() , а
также времени
, а
также времени ![]() . Следовательно, полный дифференциал
скорости
. Следовательно, полный дифференциал
скорости ![]() будет
будет
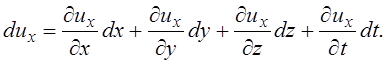 (3.62)
(3.62)
Ускорение
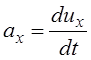 ;
;
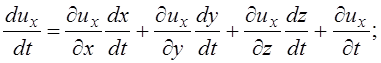
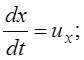
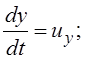
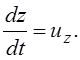
Тогда
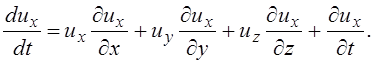 (3.64)
(3.64)
Аналогично
можно получить дифференциалы скоростей ![]() ,
, ![]() .
.
После
внесения в систему уравнений (3.61) дифференциалов скоростей ![]() ,
, ![]() и
и ![]() она примет вид
она примет вид
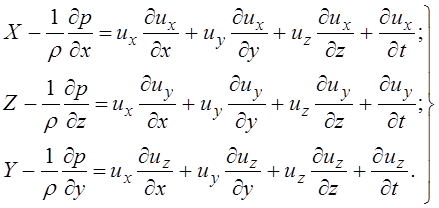 (3.65)
(3.65)
В случае установившегося движения
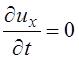 ;
; 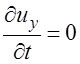 ;
; 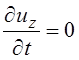 . (3.66)
. (3.66)
Уравнения (3.65) представляют собой дифференциальные уравнения движения идеальной (невязкой) жидкости - уравнения Эйлера. Эти уравнения были получены Эйлером в 1775 г.
Уравнения Эйлера выражают связь между проекциями действующих сил, скоростей, давления и плотности жидкости. Уравнения Эйлера очень важны при изучении движения жидкости.
Для жидкости, находящейся в покое, имеем
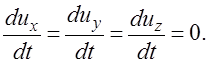
Дифференциальные уравнения Эйлера приобретают следующий вид:
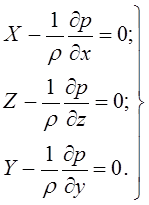 (3.67)
(3.67)
Система дифференциальных уравнений является уравнениями равновесия жидкости.
Из уравнения равновесия можно получить основное уравнение гидростатики (2.2) (см. приложение).
Интегрирование уравнения движения Эйлера. Интеграл Бернулли
Рассмотрим
установившееся движение идеальной жидкости. Уравнения Эйлера представим в виде
(3.61). Умножим первое из уравнений на ![]() , второе - на
, второе - на ![]() и третье - на
и третье - на ![]() , получим
, получим
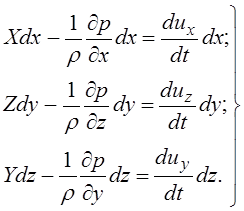 (3.68)
(3.68)
Сложим почленно все три уравнения системы:
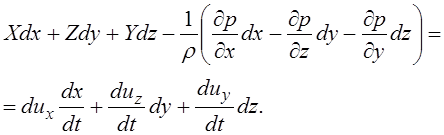 (3.69)
(3.69)
Для
установившегося движения давление ![]() в точке является
функцией ее координат и не зависит от времени. Поэтому дифференциал давления
выражается в частных производных:
в точке является
функцией ее координат и не зависит от времени. Поэтому дифференциал давления
выражается в частных производных:
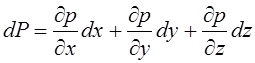 .
.
Так как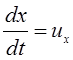 ;
; 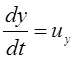 и
и 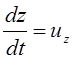 , то последний член уравнения (3.69)
, то последний член уравнения (3.69)
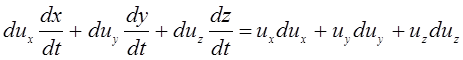 , (3.70)
, (3.70)
кроме того
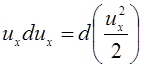 ;
; 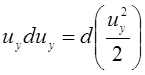 ;
; 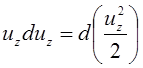 .
.
Следовательно, правая часть уравнения (3.69) примет вид
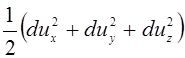 . (3.71)
. (3.71)
Полная
(абсолютная) скорость и выражается через ![]() ,
, ![]() ,
, ![]() :
:
![]() .
.
Тогда
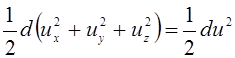 . (3.72)
. (3.72)
Уравнение (3.69) после преобразования можно переписать в следующем виде:
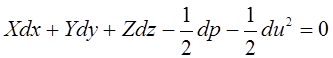 . (3.73)
. (3.73)
Первые
три выражения в этом уравнении является полным дифференциалом силовой
(потенциальной) функции![]() :
:
![]() . (3.74)
. (3.74)
Таким образом, уравнение (3.74) примет вид
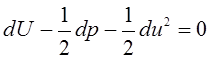 . (3.75)
. (3.75)
Проинтегрировав уравнение (3.75), получим
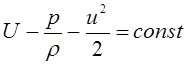 . (3.76)
. (3.76)
Данное выражение называют интегралом Бернулли-Эйлера.
Полученный трехчлен - уравнения сохраняет неизменное значение вдоль линии тока.
В случае
когда движение происходит под действием только одной массовой силы - силы
тяжести, то единичные массовые силы![]() ,
, ![]() ,
, ![]() (ось
(ось ![]() направлена вертикально вверх).
Дифференциал силовой функции
направлена вертикально вверх).
Дифференциал силовой функции
![]() . (3.77)
. (3.77)
Уравнение (3.75) можно написать в следующем виде:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.