Задачи кинематики и динамики. Основные понятия и определения струйчатой модели движения жидкости. Приборы для измерения скорости и расхода жидкости, страница 7

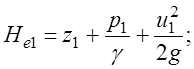
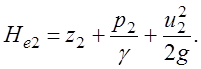
Потери удельной механической энергии, обусловленные трением, на участке живых сечений 1-1 и 2-2

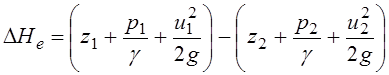                 (3.45)

или

                                     (3.46)

Таким образом, уравнение Бернулли для элементарной струйки реальной жидкости в случае установившегося движения можно представить в виде

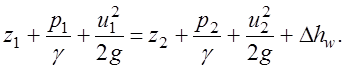                           (3.47)

Характеристикой движения жидкости является понятие пьезометрического и гидравлического уклонов.

На рис. 3.8 изображены кривые, характеризующие уравнение Бернулли. Линия, проходящая через точки, соответствующие значению пьезометрической высоты в живых сечениях 1-1 и 2-2, является пьезометрической линией.

Пьезометрическим уклоном называется изменение гидростатического напора жидкости вдоль струйки, отнесенное к единице длины. На участке струйки длиной  между сечениями 1-1 и 2-2 пьезометрический уклон

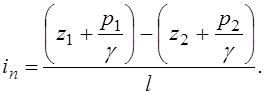                               (3.48)

Пьезометрический уклон, соответствующий бесконечно малой длине  (при ), - уклон в точке:

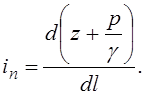                                                   (3.49)

Линия, проходящая через точки значений удельных механических энергий в живых сечениях струйки, является напорной линией (линией полного напора). Гидравлическим уклоном называется уменьшение полной удельной механической энергии вдоль струйки, отнесенное к единице длины:

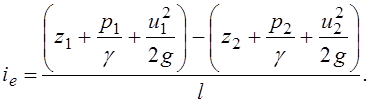             (3.50)

При элементарном снижении удельной энергии  на бесконечно малом участке  гидравлический уклон

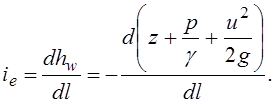                   (3.51)

Так как кривая полного напора убывает по длине струйки, то знак в выражении (3.51) минус [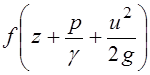 - убывающая функция].

В случае постоянства живых сечений по длине струйки пьезометрическая линия и линия полного напора параллельны.

3.9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ (УРАВНЕНИЕ ЭЙЛЕРА)

В пространстве, заполненном движущейся идеальной жидкостью плотностью , выделим элементарный параллелепипед, ребра которого со сторонами , ,  параллельны осям координат (рис. 3.9). При движении идеальной жидкости отсутствуют силы внутреннего трения. Элементарный объем, находящийся в параллелепипеде, перемещается с абсолютной скоростью . Составляющие этой скорости по осям координат будут , , .

На элементарный объем будут действовать массовые и поверхностные силы. Силы трения при движении параллелепипеда равны нулю.

Масса жидкости в элементарном объеме параллелепипеда

                                                   (3.52)

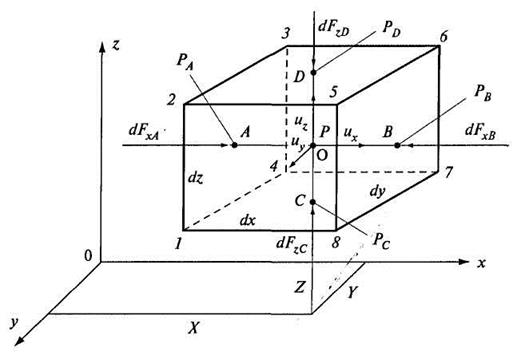
Рис. 3.9. К выводу уравнения движения Эйлера

Проекции массовых сил в направлении координатных осей:

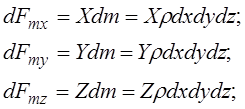                                   (3.53)

где , ,  - компоненты единичных массовых сил относительно осей , ,  (проекции ускорения этих сил).

Поверхностные силы определяются давлением, приходящимся на грани параллелепипеда.

Пусть в центре тяжести параллелепипеда (т. О) гидростатическое давление равно , координаты этой точки , , . Скорость движения в этой точке . Составляющие этой скорости по осям координат равны , , .

Проведем через т. О горизонтальную линию, параллельную оси . Точки пересечения с гранями параллелепипеда А (грань 1234), В (грань 5678). Давление в этих точках по оси   и .

В жидкой сплошной среде давление в точке выражается непрерывной сплошной функцией координат расположения точки в пространстве: . Гидростатическое давление изменяется непрерывно линейно, и приращение давления на единицу элементарной длины  -   -   -

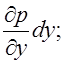
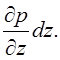
Следовательно, давления в точках А и В будут различаться на величину .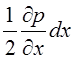

Давления в точках А и В выразим в следующем виде:

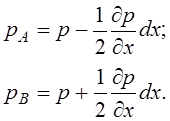                                               (3.54)

Из-за малости площади граней можно считать, что давления  и  являются средними гидростатическими давлениями, действующими на грани 1234 и 5678. Поверхностные силы давления на эти грани по оси  равны произведению давления на площади граней:

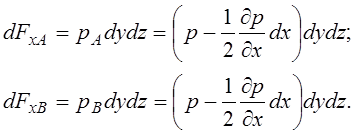                (3.55)

Аналогично поверхностные силы давления на грани по оси z (грани 1478и 2365):

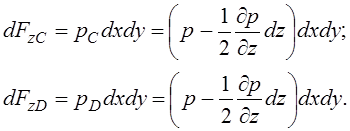                 (3.56)