Задачи кинематики и динамики. Основные понятия и определения струйчатой модели движения жидкости. Приборы для измерения скорости и расхода жидкости, страница 11

Коэффициент Буссинеска - отношение фактического количества движения к условному .

Количество движения, выраженное через среднюю скорость,

.                                                (3.99)

Для турбулентных потоков на основании опытных исследований .

На практике при решении гидравлических задач обычно коэффициент Буссинеска не учитывается, т.е. принимается .

Средние скорости в сечениях равны, и , тогда количество движений для массы элементов участков:

;

.                                          (3.100)

Изменение количества движения

.                                  (3.101)

Относительно оси

.                               (3.102)

Рассмотрим все внешние силы и импульс, действующие на объем жидкости, находящийся между сечениями 1-1 и 2-2.

•    Силы давления, действующие на торцы сечений 1-1 и 2-2,определяются силами и. Проекция импульса сил давления на ось

.                                                     (3.103)

•    Сила тяжести выделенного объема жидкости . Проекция импульса сил давления на ось

.                                                                 (3.104)

•    Силы реакции боковых стенок, ограничивающих рассматриваемый объем жидкости, равны . Проекция импульса сил реакций стенок на ось

.                                                                 (3.105)

•    Сила внешнего трения, воздействующая на внутренние стороны боковых стенок, - . Проекция импульса сил внешнего трения на

.                                                                (3.106)

Таким образом, импульс на ось

.                   (3.107)

Уравнение изменения количества движения в гидравлической форме согласно (3.102) и (3.107) имеет следующий вид:

.       (3.108)

Уравнение изменения количества движения в гидравлическом виде можно сформулировать следующим образом.

Изменение количества движения потока жидкости при переходе от плоского живого сечения 1-1 к плоскому живому сечению 2-2 за единицу времени относительно выбранной координатной оси равно сумме проекции внешних сил на ось, действующих на объем жидкости между сечениями 1-1 и 2-2.

3.12. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ УРАВНЕНИЯ БЕРНУЛЛИ

Расходомер Вентури

Расходомер Вентури представляет собой плавно суженную и расширяющуюся цилиндрическую вставку, устанавливаемую в трубе. Чтобы понять принцип его работы, рассмотрим рис. 3.13. Установим два пьезометра: один в расширенной части расходомера, другой - в сужении. Приведенные далее рассуждения должны показать, что при изменении расхода жидкости, проходящей по трубопроводу, меняется разность показаний пьезометров.

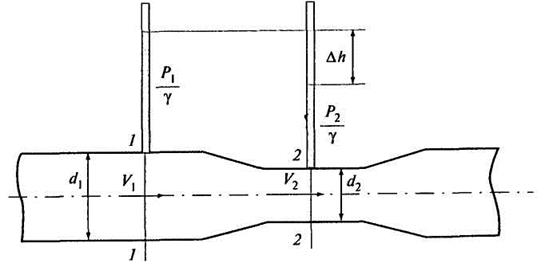
Рис. 3.13. Расходомер Вентури

Напишем уравнение Бернулли для сечений 1-1 и 2-2, полагая отсутствие потерь напора, :

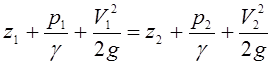.                            (3.109)

Поскольку, следовательно, показания пьезометра в первом сечении будут больше, чем во втором:

.

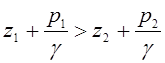Разность показаний пьезометров составляет

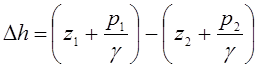.                               (3.110)

Подставив выражение (3.110) в уравнение (3.109), получим

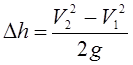.                                                     (3.111)

Поскольку площади поперечных сечений 1-1 и 2-2 известны, то, используя уравнение неразрывности для несжимаемой жидкости, имеем

,

или

.

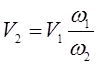Подставив полученное выражение для , в уравнение (3.111) и решив его относительно скорости , получим

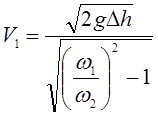.                                                (3.112)

Теоретический расход жидкости в трубопроводе составляет

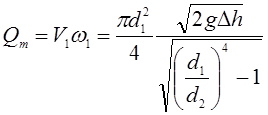.                             (3.113)

или

,

где  - постоянная расходомера.

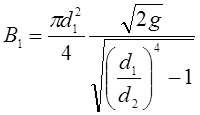.                                        (3.114)

Таким образом, если известны диаметр трубы и диаметр сужения и измерена разность пьезометрических высот, то можно вычислить расход жидкости, проходящей по трубопроводу по формуле (3.113).

Следует отметить, что в случае движения идеальной жидкости приведенные ранее рассуждения правильны. При движении через расходомер вязкой жидкости возникают потери напора, поэтому необходимо ввести в конечную формулу соответствующую поправку на сопротивление в виде коэффициента расхода водомера , .