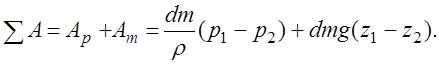 (3.39)
(3.39)
Приращение кинетической энергии равно изменению энергии массы объема жидкости 1'-2' и объема 1-2. Вычитаем из кинетической энергии массы объема 1'-2' энергию первоначального объема 1-2:
![]()
В энергии массы объемов жидкости входит энергия средней части объема 1'-2:
![]()
![]()
![]()
Массы
жидкости в отрезках струйки 2-2' и 1-1' равны, а скорости в сечениях - ![]() и
и ![]() . Таким образом, приращение кинетической энергии
. Таким образом, приращение кинетической энергии
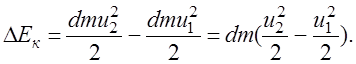 (3.40)
(3.40)
Согласно теореме кинетической энергии (3.27) получим
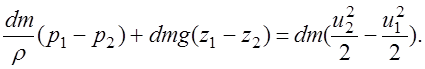 (3.41)
(3.41)
Отнесем
все члены уравнения к единице веса ![]() протекающей жидкости, т.е. разделим все члены уравнения
(3.41) на
протекающей жидкости, т.е. разделим все члены уравнения
(3.41) на ![]() :
:
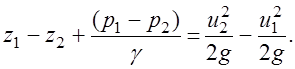 (3.42)
(3.42)
Произведем перегруппировку членов уравнения (3.42) применительно к каждому из сечений 1-1 и 2-2:
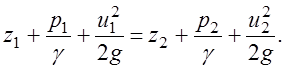 (3.43)
(3.43)
Полученное уравнение называется уравнением Д. Бернулли для струйки идеальной жидкости.
Все
члены уравнения Бернулли имеют линейную размерность. Члены уравнения ![]() , и
, и ![]() - геометрические
высоты положения центров живых сечений относительно плоскости сравнения.
- геометрические
высоты положения центров живых сечений относительно плоскости сравнения.
Установив
пьезометры в сечениях 1-1 и 2-2, уровень жидкости в них поднимается на высоты 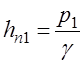 и
и 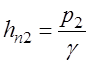 . Члены
. Члены
![]() и
и ![]() пьезометрические высоты, которые
соответствуют гидростатическим давлениям
пьезометрические высоты, которые
соответствуют гидростатическим давлениям ![]() и
и ![]() в сечениях 1-1 и 2-2.
в сечениях 1-1 и 2-2.
Члены
уравнения ![]() и
и ![]() - скоростные высоты.
- скоростные высоты.
Сумма всех трех членов уравнения вдоль струйки постоянна:
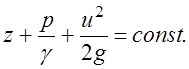
Ранее приводилось понятие удельной энергии. Энергия жидкости, отнесенная к единице веса жидкости, - удельная энергия или напор. Полная энергия струйки складывается из потенциальной и кинетической энергий.
Первых
два члена уравнения Бернулли характеризуют потенциальную энергию относительно
плоскости сравнения 0-0. Третий член ![]() выражает кинетическую энергию. Таким
образом, сумма всех членов уравнения будет являться суммой удельных
потенциальной и кинетической энергий.
выражает кинетическую энергию. Таким
образом, сумма всех членов уравнения будет являться суммой удельных
потенциальной и кинетической энергий.
Полная
удельная энергия ![]() - полный напор, определяемый по формуле
- полный напор, определяемый по формуле
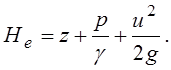 (3.44)
(3.44)
Полная
удельная механическая энергия для идеальной жидкости вдоль элементарной струйки
является постоянной величиной - ![]() .
.
Члены уравнения Бернулли имеют следующую энергетическую интерпретацию:
![]() -
удельная энергия положения;
-
удельная энергия положения;
![]() - удельная
потенциальная энергия давления;
- удельная
потенциальная энергия давления;
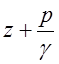 - удельная
потенциальная энергия, гидростатический напор;
- удельная
потенциальная энергия, гидростатический напор;
![]() - удельная кинетическая энергия или динамический
(скоростной) напор.
- удельная кинетическая энергия или динамический
(скоростной) напор.
Удельная потенциальная или кинетическая энергия в разных сечениях по длине струйки могут изменять свои величины, однако сумма их вдоль рассматриваемой идеальной струйки жидкости остается постоянной.
Если все
члены умножить на единицу веса ![]() , то получим сумму полной механической энергии, которая будет
постоянна для всех сечений.
, то получим сумму полной механической энергии, которая будет
постоянна для всех сечений.
Таким образом, уравнение Бернулли для струйки идеальной жидкости при ее установившемся движении выражает закон сохранения механической энергии.
3.8. УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ СТРУЙКИ РЕАЛЬНОЙ ЖИДКОСТИ
Реальная
жидкость обладает вязкостью, и при ее движении возникают сопротивления
движения. Сопротивления движения обусловлены появлением сил внутреннего трения.
При движении струйки реальной жидкости механическая энергия, содержащаяся в
струйке, вдоль нее будет уменьшаться, так как часть ее будет расходоваться на
преодоление сопротивления, ![]() .
.
Эта энергия затрачивается на некоторую необратимую работу, т.е. на работу сил трения, и она переходит в тепло, которое рассеивается.
Чем больше длина струйки, тем больше будут затраты энергии на преодоление сопротивления движения.
Энергия,
расходуемая на работу сил трения, - потери механической энергии
струйки, переходящие в теплоту. Потери энергии, отнесенные к единице веса
жидкости при перемещении ее вдоль элементарной струйки, называются
гидравлическими потерями (потерями удельной энергии) ![]() .
.
Рассмотрим струйку реальной жидкости при установившемся движении (рис. 3.8).
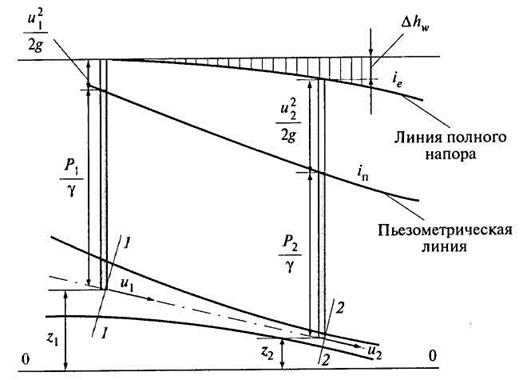
Рис. 3.8. К уравнению Бернулли для струйки реальной жидкости
Полная удельная механическая энергия реальной струйки в ее живых сечениях 1-1 и 2-2 составит
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.