Последний интеграл в зависимости (3.83) характеризует потери механической энергии в потоке на участке 1-2, т.е. потери энергии, утрачиваемые струйками на работу сил трения. Средняя потеря энергии на участке потока жидкости
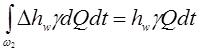 (3.89)
(3.89)
где 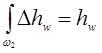 - удельные потери энергии.
- удельные потери энергии.
С учетом вышеизложенного уравнение (3.83) можно выразить следующим образом:
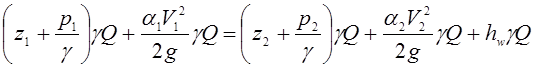 . (3.90)
. (3.90)
Разделив
левую и правую части выражения (3.90) на единицу веса жидкости ![]() за время
за время ![]() , получим
, получим
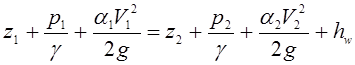 . (3.91)
. (3.91)
Данное уравнение (3.91) является уравнением Бернулли для конечного потока реальной жидкости.
Значения
![]() и
и ![]() -
коэффициенты кинетической энергии, зависящие от неравномерности распределения
скоростей по живым сечениям 1-1 и 2-2 потока.
-
коэффициенты кинетической энергии, зависящие от неравномерности распределения
скоростей по живым сечениям 1-1 и 2-2 потока.
Сумма
членов уравнения (3.91) 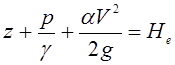 - полная удельная механическая энергия потока;
- полная удельная механическая энергия потока; ![]() - удельная энергия положения живого
сечения;
- удельная энергия положения живого
сечения; ![]() - удельная энергия давления в живом
сечении потока;
- удельная энергия давления в живом
сечении потока; 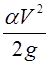 - удельная кинетическая энергия
потока, динамический (скоростной) напор;
- удельная кинетическая энергия
потока, динамический (скоростной) напор; 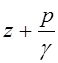 - удельная
потенциальная энергия, гидростатический напор;
- удельная
потенциальная энергия, гидростатический напор; ![]() - потери
удельной энергии на участке, потери напора.
- потери
удельной энергии на участке, потери напора.
Уравнение Бернулли для потока реальной жидкости является уравнением баланса механической энергии с учетом ее потерь. Энергия, затрачиваемая на работу сил трения, превращается в тепловую, которая рассеивается в потоке и влечет за собой некоторое увеличение температуры жидкости потока.
3.11. ТЕОРЕМА ИЗМЕНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ ДЛЯ ПОТОКА ЖИДКОСТИ
При решении некоторых гидравлических задач использования уравнения Бернулли недостаточно, и в этих случаях применяется теорема об изменении количества движения материальной точки.
Количеством
движения материальной точки называется произведение ее массы ![]() на скорость ее движения
на скорость ее движения ![]() . Количество движения
. Количество движения ![]() является вектором, направление которого
совпадает с направлением движения, т.е. со скоростью. Количество движения, зависящее
от массы и ее скорости, является мерой механического движения. Понятие
количества движения (КД) положено в основу механики Ньютона.
является вектором, направление которого
совпадает с направлением движения, т.е. со скоростью. Количество движения, зависящее
от массы и ее скорости, является мерой механического движения. Понятие
количества движения (КД) положено в основу механики Ньютона.
Тело
массой ![]() под действием сил переместится в другое положение
за определенное время
под действием сил переместится в другое положение
за определенное время ![]() , и скорость тела изменится
, и скорость тела изменится ![]() до
до ![]() .
.
Изменение
количества движения ![]()
![]() . (3.92)
. (3.92)
За этот промежуток времени на тело будет действовать импульс сил
![]() . (3.93)
. (3.93)
Теорема
количества движения сформулирована следующим образом. Изменение количества движения материальной
точки за некоторый промежуток времени равно сумме импульсов сил, приложенных к
точке, за этот же промежуток времени, ![]() :
:
![]() . (3.94)
. (3.94)
Теорема количества движения называется также теоремой импульсов.
Применим
данную теорему к участку потока между сечениями 1-1 и 2-2 при установившемся
движении потока жидкости расходом ![]() в определенный
промежуток времени (рис. 3.12). За время
в определенный
промежуток времени (рис. 3.12). За время ![]() участок
между сечениями 1-1 и 2-2 переместится в положение, определяемое сечениями 1'-1'
и 2'-2'. Изменение количества движения
участок
между сечениями 1-1 и 2-2 переместится в положение, определяемое сечениями 1'-1'
и 2'-2'. Изменение количества движения
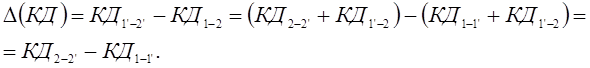 (3.95)
(3.95)
Масса элементов участков 1-1' и 2-2' на рисунке заштрихованы. Так как стенки потока непроницаемы, то согласно уравнению неразрывности массы этих элементов одинаковы:
![]() . (3.96)
. (3.96)
Масса, проходящая через сечения,
![]() .
.
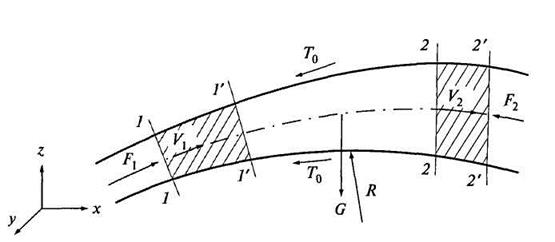
Рис. 3.12. К теореме количества движения для потоков жидкости
Если в живом сечении местные скорости в разных его точках различны, то количество движения
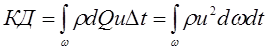 , (3.97)
, (3.97)
где ![]() -
скорость в определенной точке сечения, местная скорость.
-
скорость в определенной точке сечения, местная скорость.
При
предположении, что скорости во всех точках живого сечения равны средней
скорости ![]() , вводится коэффициент Буссинеска
, вводится коэффициент Буссинеска ![]() (коэффициент количества движения)
(коэффициент количества движения)
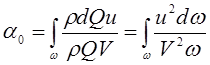 . (3.98)
. (3.98)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.