Теоретические основы электротехники. Электротехника: Контрольные задания с методическими указаниями

Примечание:

         Ниже приведена только часть методического пособия.

            авторы: Зима Т.Е, Морозова Т.В., Нейман В.Ю.        

      Сокращения, с разрешения авторов, выполненны Лаппи Ф.Э.

4. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

К РАСЧЕТУ СЛОЖНЫХ ЦЕПЕЙ

Сложной электрической цепью называют цепь, которая содержит пассивные двухполюсники, не образующие последо­вательного и параллельного соединений (см. рис. 4.1).

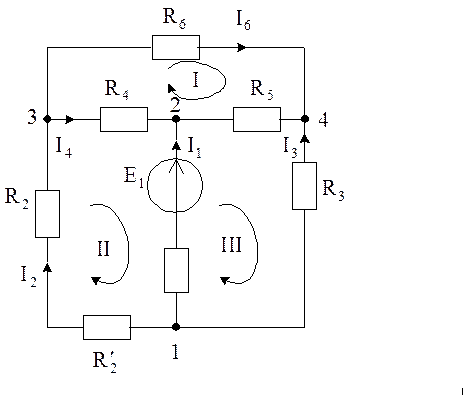
Рис. 4.1

Основными методами расчета сложных цепей являются: метод токов ветвей (составление уравнений по законам Кирхгофа), метод контурных токов и метод узловых потенциалов.

Наиболее рациональным методом является метод, применяя который получают для расчета токов наименьшее число уравнений.

Методы контурных токов и узловых потенциалов уменьшают полное число уравнений, необходимых для расчета токов и поэтому, являются наиболее рациональными при расчете сложных цепей.

4.1. Метод контурных токов

Согласно методу предполагается, что в каждом независимом контуре  протекает свой контурный ток. 

Независимыми называются контуры, которые имеют хотя бы одну новую ветвь, не входящую в другие контуры.

Число независимых контуров схемы равно числу уравнений, которые нужно составить по второму закону Кирхгофа:

,

где  – число ветвей схемы,  – число узлов,  – число источников тока. В схеме, представленной на рис. 4.1, число независимых контуров  . 

Предположение о контурных токах приводит к тому, что число неизвестных, и, соответственно, число уравнений, необходимых для определения этих неизвестных, уменьшается по сравнению с полной системой уравнений Кирхгофа и равно числу уравнений, которые нужно составить по второму закону Кирхгофа , т.е. числу независимых контуров. Этот метод основан на законах Кирхгофа. Он является, фактически, записью законов Кирхгофа через контурные токи.  Пусть имеем схему, содержащую   независимых контуров.  Согласно методу контурных токов в каждом -м независимом контуре протекает контурный ток  .  В общем случае система уравнений для расчета контурных токов имеет вид:

                (4.1)

,

где  – полное (собственное)  сопротивление  -го контура, равное сумме всех сопротивлений, входящих в этот контур,

 – общее (смежное) сопротивление -го  и  -го контуров,

 – для линейных цепей.

Полное сопротивление   всегда больше нуля: .

, если контурные токи в общей (смежной)  ветви протекают (направлены) согласно, и  ,если контурные токи направлены встречно.

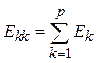 – алгебраическая сумма ЭДС, входящих в -й контур.

Со знаком «плюс» берутся ЭДС, направление которых совпадает с контурным током  , а со знаком  «минус» направление которых не совпадают  с  .

Контурные токи можно рассчитать, используя теорию определителей:

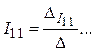
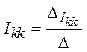   ,                       (4.2)

где главный определитель системы:

;

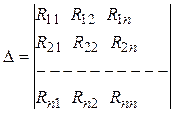алгебраическое дополнение к контурному току :

.

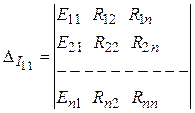Истинный ток (искомый ток) в любой ветви равен алгебраической сумме  контурных токов, протекающих по этой ветви. Со знаком «плюс» берутся контурные токи, совпадающие с истинным током; со знаком «минус» – несовпадающие с искомым током. Система уравнений (4.1) записана в предположении, что источники энергии можно представить, как источники ЭДС (схема содержит только источники ЭДС:).

При наличии в электрической схеме реальных источников тока они могут быть заменены эквивалентными источниками ЭДС.

Если схема содержит идеальные  источники тока, то целесообразно выбрать задающие токи источников тока в качестве контурных токов. В этом случае число неизвестных контуров токов и, соответственно, число уравнений сокращается на число задающих токов

().

Если в заданной схеме имеются параллельные ветви, не содержащие источников ЭДС, то замена их эквивалентным сопротивлением сокращает число контуров за счет тех, которые образованы параллельными ветвями.

Метод контурных токов целесообразно применять, когда схема содержат много узлов, но мало независимых контуров.

4.2. Метод узловых потенциалов

Метод контурных токов позволяет исключить из полной системы уравнений Кирхгофа все уравнения, составленные по первому закону Кирхгофа и сохранить уравнения только для независимых контуров.

Метод узловых потенциалов позволяет сохранить только те  уравнения Кирхгофа, которые составлены для узлов, и исключить уравнения для контуров, составленные по 2-му закону Кирхгофа.

Метод узловых потенциалов рационально применять, когда в схеме узлов меньше, чем независимых контуров.

В основе метода узловых потенциалов лежит первый закон Кирхгофа и закон Ома для участка цепи с ЭДС.

Пусть схема имеет число узлов . Число уравнений, которые должны быть составлены по 1-му закону Кирхгофа, равно .

Столько уравнений необходимо составить и по методу узловых потенциалов, принимая потенциал одного из узлов равным нулю.

Пусть . В общем виде уравнения, составленные по методу узловых потенциалов, имеют вид: