Электрические цепи однофазного синусоидального тока

сумма одних векторов была равна сумме других векторов токов; а сумма векторов падений напряжения в некотором контуре была равна сумме векторов ЭДС, действующих в этом контуре. Если же векторы напряжений располагать ещё и в том же порядке, как они следуют в контуре,  то  каждой  точке ВД будет соответствовать некоторая точка схемы, и тогда можно будет производить по ВД ещё и измерения некоторых невычисленных напряжений.

3.4. R, L, C  - элементы в цепях синусоидального тока

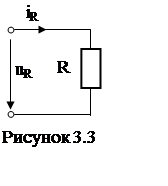3.4.1. Резистивный элемент R (рис. 3.3)

Пусть ток   i_R (t) = I_m sin (wt+y_i). Природа сопротивления R протеканию электрического тока такова, что оно не вызывает между током и напряжением сдвига по фазе. Поэтому связь между током и напряжением здесь подчиняется закону Ома в любой момент времени:

u_R(t) = R I_m sin (wt+y_i) = U_Rm sin (wt+y_u).

Мгновенная мощность – это произведение мгновенных значений напряжения и тока:

p_R(t)=u_R(t)i_R(t)=U_Rm I_m sin²(wt+y_i)=UI[1-cos(2wt+2y_i)]=

= U I – U I cos(2wt+2y_i).

Активной мощностью цепи переменного тока принято называть среднее за период значение мгновенной мощности. В данном случае активная мощность P = U I = R I², то есть вычисляется по той же формуле, что и в цепях постоянного тока.  

  По полученным соотношениям можно построить ВД (рис. 3.4).

3.4.2. Индуктивный элемент L (рис. 3.5)

Индуктивность оказывает сопротивление переменному току тем, что в ней возникает ЭДС самоиндукции, которая задерживает изменение тока, то есть заставляет его отставать по фазе от изменяющегося напряжения. Возможны моменты, когда напряжение уже есть, а ток равен нулю. В таком случае законом Ома воспользоваться нельзя. Поэтому напряжение  u_L(t)  будем находить по закону электромагнитной индукции:

u_L(t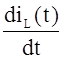) = L  = L  [ I_m sin(wt+y_i)] = L w I_Lm cos(wt+y_i) =

= x_L I _msin(wt+y_i + 90^o) = U_m sin(wt+y_i).

Здесь величина   x_L = wL [Гн =  Ом с = Ом] обладает размерностью сопротивления и поэтому называется индуктивным (реактивным) сопротивлением синусоидальному переменному току.

Отметим, однако, что закон Ома, несправедливый для мгновенных значений, выполняется для действующих значений и амплитуд:   u_L(t) ¹ x_L i_L(t),    U_L = x_L I_L ,    U_Lm = x_L I_Lm .

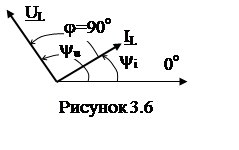
Наконец,  видим, что по фазе напряжение на индуктивности опережает ток на +90^о: y_u= y_i + 90^o.

p_L(t) = u_L(t) i_L(t) = U_L I_L sin(wt+y_u) sin(wt+y_i) =

= 2 U_L I_L  [cos (a-b) – cos (a+b)] = U_L I_L [ - cos(2wt+2y_i +90^o)] =

= U_L I_L sin [2(wt+y_i)] .

Мгновенная мощность индуктивного элемента является чистой синусоидой, но удвоенной частоты.   Следовательно,   активная   мощность в индуктивности не выделяется: P_L = 0.  Такие элементы называются реактивными.

Векторная диаграмма имеет вид рис. 3.6.

3.4.3. Ёмкостный элемент C (рис. 3.7)

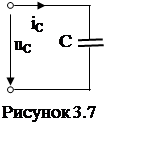Выражение для тока найдём как изменение заряда ёмкости во времени. Будем считать напряжение заданным: u_С(t) =U_Cm sin(wt+y_u).

i_C(t)=  = C 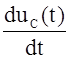 = C wU_Cm cos(wt+y_u) =

=  U_Cm sin(wt+y_u + 90^o) = I_Cm sin(wt+y_i).

Синусоидальному току ёмкость оказывает сопротивление, равное

x_C =  =  [ ].

Закон Ома справедлив лишь для действующих и амплитудных значений, так как ток i_C(t) и напряжение  u_C(t) сдвинуты по фазе на 90^о, причём напряжение отстаёт от тока:   y_u = y_i  - 90^o.

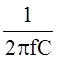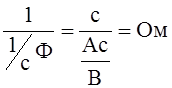p_С(t) = u_С(t) i_С(t) = U_Cm I_Cm sin(wt+y_u) sin(wt+y_i) =U_C I_C sin[2(wt+y_u)] .

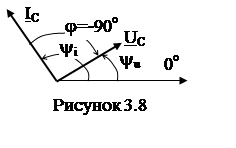
P_C = 0, то есть емкость – реактивный элемент, а векторная диаграмма имеет вид рис. 3.8.

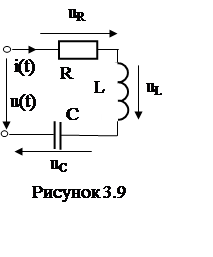
3.4.4. Последовательное включение R, L, C элементов (рис. 3.9)

Пусть i(t) = I_m sin(wt+y_i).

Входное напряжение цепи найдём по П закону Кирхгофа:

u(t) = u_R + u_L + u_C  = R I_m sin(wt+y_i) + x_L  I_m sin(wt+y_i + 90^o) +

+ x_С I_m sin(wt+y_i – 90^o) = I_m [R sin(wt+y_i) + (x_L – x_C ) cos(wt+y_i)] =

=  I_m sin(wt+y_i +j) = Z I_m sin(wt+y_i +j) = U_m sin(wt+y_u),

так как   m sina  n cosa = sin (aj), причём

j = arctg  = arctg .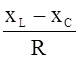

Получим теперь выражения для мгновенной и активной мощностей цепи:

p(t) = u(t) i(t) = U_m I_m sin(wt+y_u) sin(wt+y_i) =

= U I [cos (a-b) – cos (a+b)] =

= U I cosj  - U I cos(2wt+2y_i+j).

P = 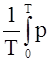(t)dt = U I cosj = Z I I cosj = R I².

Таким образом, для цепи с последовательным соединением R, L, C справедливы следующие расчётные соотношения:

- полное сопротивление цепи  Z = ,

- сдвиг по фазе между  напряжением и током  j = y_u - y_i = arctg,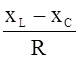

- закон Ома  U_m = Z I_m , U = Z I,

- второй закон Кирхгофа    U = ,

- активная мощность цепи    P = U I cos j = R I².

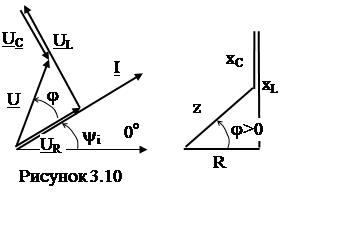На основании полученных соотношений можно построить ВД и треугольник сопротивлений цепи (рис. 3.10). Они построены для случая  x_L >x_C. При этом

R = Z cos j;    x = x_L – x_C = Z sinj;      U_a = R I;       U_p = (x_L – x_C) I = x I.

3.4.5. Параллельное включение R, L, C (рис. 3.11)

Пусть u(t) = U_m sin(wt+y_u).

Входной ток определим по I закону Кирхгофа:

i(t) = i_R + i_L + i_C  =

=  U_m sin(wt+y_u) +  U_m sin(wt+y_u- 90^o) +

+  U_m sin(wt+y_u + 90^o) = U_m [g sin(wt+y_u) –

 - (b_L – b_C ) cos(wt+y_u)] =  U_m sin(wt+y_u - j) = Y U_m sin(wt+y_u - j) =

= I_m sin(wt+y_i),

причём   j = y_u - y_i = arctg .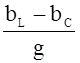

P = 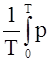(t)dt = U I cosj = U Y U cosj = g U².

Таким образом, для цепи с параллельным соединением R, L, C расчётные соотношения записываются через проводимости:

- проводимости – активная -  g =   ,

                               реактивные – b_L = 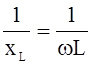;     b_C = ;

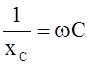                               полная –  Y = ,

- закон Ома   I_m = Y U_m , I = Y U,

- активная и реактивная составляющие тока