Метод эквивалентного генератора (эквивалентного источника). Применение математической программной среды MathCAD для расчета линейных цепей постоянного тока (главы 6-10 учебного пособия "Теоретические основы электротехники в примерах и задачах")

6. МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА

(ЭКВИВАЛЕНТНОГО ИСТОЧНИКА)

Целесообразность использования данного метода становится очевидной, в случае если расчет электрической цепи ограничен в определении тока только одной ветви. В этом случае вся цепь относительно ветви с интересующим током заменяется эквивалентной схемой. Таким образом, основной расчет сводится к определению двух параметров эквивалентной схемы – ЭДС и сопротивления эквивалентного генератора.

Задача 6.1.

Для схемы цепи (рис. 6.1) методом эквивалентного генератора найти ток ветви с сопротивлением , если , ,  , , , , .

            

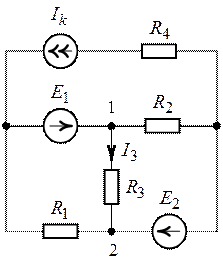
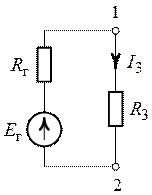
    Рис. 6.1.                                      Рис. 6.2.

Решение.

1. Выделим ветвь с сопротивлением  и обозначим ток  (рис.6.1) .

2. Всю цепь, рис. 6.1, относительно ветви с сопротивлением , представим эквивалентным генератором с источником ЭДС равным  и сопротивлением  (рис. 6.2).

Согласно схеме (рис. 6.2) интересующий ток в ветви определиться как

,

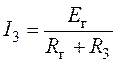т.е. решение задачи сводится к определению двух параметров эквивалентного генератора  и .

3. Найдем ЭДС генератора. По определению  равно напряжению  между узловыми точками 1 и 2 разомкнутой ветви с сопротивлением  (рис. 6.3).

              

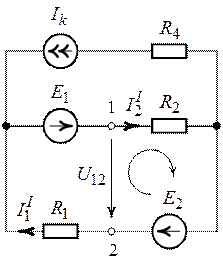
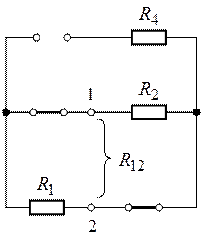
Рис. 6.3.                                             Рис. 6.4.

Для этого в схеме (рис. 6.3) определим токи  и . На основании законов Кирхгофа получим систему:

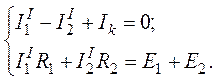
Из системы найдем

,

.

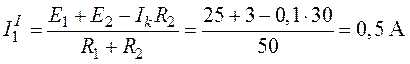На основании второго закона Кирхгофа для указанного в схеме (рис. 6.3) направления обхода контура получим

.

4. Найдем сопротивление генератора. По определению  равно входному сопротивлению  между узловыми точками 1 и 2 разомкнутой ветви с  (рис. 6.3). Расчет сопротивления  производим при закороченных источниках ЭДС ,  и разомкнутом источнике тока , рис. 6.4.

.

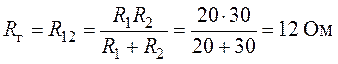5. Окончательно определяем ток :

.

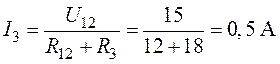Задача 6.2.

Определить методом эквивалентного генератора ток в ветви с источником ЭДС  (рис. 6.5). Дано: , , , , , , .

              

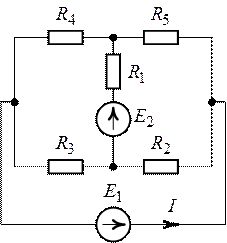
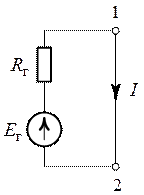
          Рис. 6.5.                                           Рис. 6.6.

Решение

1. Обозначим ток  в ветви с источником ЭДС  (рис. 6.5).

2. Применив теорему об эквивалентном генераторе, ток в ветви, имеющей нулевое сопротивление согласно схеме (рис. 6.6):

.

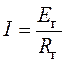3. Найдем ЭДС генератора. Разомкнем ветвь с источником  (рис.6.7) и найдем напряжение  между точками 1 и 2.

Предварительно выполним расчет токов  и  в схеме (рис. 6.7).

             

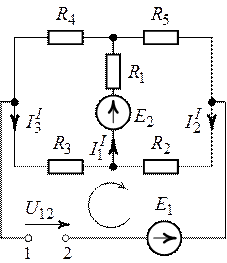
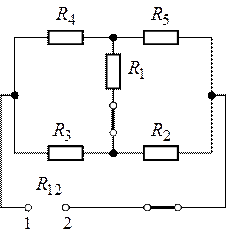
Рис. 6.7.                                             Рис. 6.8.

Ток  в неразветвленной  части схемы

.

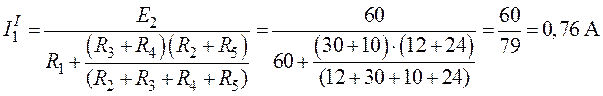Токи  и  в разветвленной части схемы:

;

.

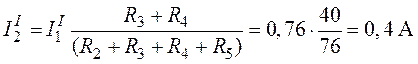На основании второго закона Кирхгофа для обозначенного на схеме (рис. 6.7) контура запишем:

,

откуда

.

4. Найдем сопротивление генератора , которое равно входному сопротивлению  между точками 1 и 2 (рис. 6.8) (при замкнутых источниках ЭДС , ).

Преобразуем треугольник сопротивлений ,  и  (рис.6.8) в эквивалентную звезду (рис. 6.9).

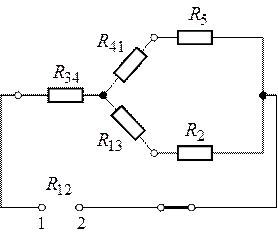
Рис. 6.9.

Величины сопротивлений эквивалентной звезды (рис. 6.9):

;

;

.

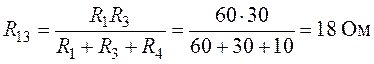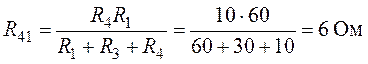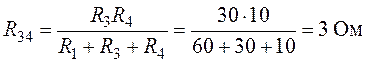Согласно выполненным преобразованиям окончательно получим (рис. 6.9):

.

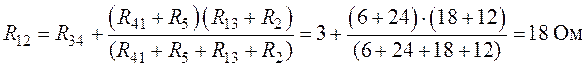5. Ток в ветви с источником  определится как

.

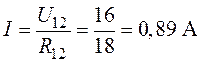Задачи для самостоятельного решения

Задача 6.3. Методом эквивалентного генератора для схемы (рис. 6.10) определить ток в ветви с сопротивлением . Дано , , , , , .

О т в е т:  (, ).

          

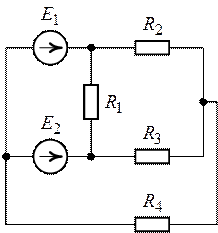
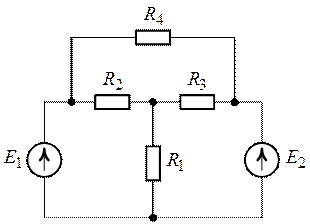
Рис. 6.10.                                                    Рис. 6.11.

Задача 6.4. Для цепи (рис. 6.11) методом эквивалентного генератора определить ток в ветви с сопротивление , если , , , , .

О т в е т:  (, )

Задача 6.5. Определить обозначенный в схеме (рис. 6.12) ток по методу эквивалентного генератора, если , , , , , , , .

О т в е т:  (, )

Задача 6.6. Для схемы (рис. 6.13) методом эквивалентного генератора определить обозначенный в ветви ток, если , , , , , .

О т в е т:  (, )

                

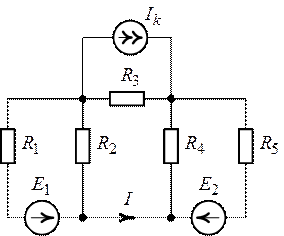
Рис. 6.12.                                                       Рис. 6.13.

Задача 6.6. Рассчитать обозначенный в схеме (рис. 6.14) ток, используя метод эквивалентного генератора, если , , , , , .

О т в е т:  (, )

Задача 6.4. Для цепи (рис. 6.15) методом эквивалентного генератора определить ток в ветви с сопротивление , если , , , , , , , , .

О т в е т:  (, )

          

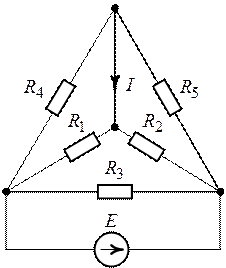
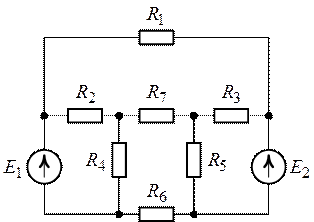
Рис. 6.14.                                                     Рис. 6.15.

7. ПРИМЕНЕНИЕ ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ ПРИ РАСЧЕТАХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Расчет сложных электрических цепей можно упростить путем различных эквивалентных преобразований активных участков схем содержащих ветви с идеальными источниками ЭДС и тока. В частях  схемы не затронутых преобразованиями должно выполняться условие  неизменности напряжений и токов ветвей. Упрощение расчета сводится, как правило, к уменьшению числа ветвей или узлов схемы и, в конечном счете, к сокращению расчетных уравнений.

Задача 7.1.

Для цепи (рис.7.1) требуется определить показание вольтметра, если , ,  , , . Внутреннее сопротивление вольтметра принять .

   

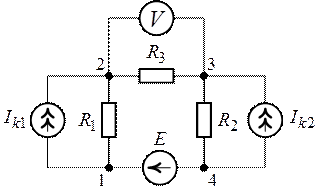
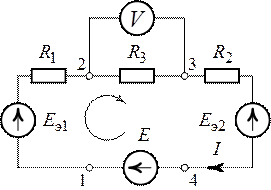
Рис. 7.1.                                         Рис. 7.2.

Решение.

1. Преобразуем источники тока  и  (рис. 7.1) в эквивалентные источники ЭДС ,  (рис. 7.2).

2. Значения ЭДС эквивалентных источников:

;  .

3. Ток, протекающий в контуре (рис. 7.2) найдем на основании второго закона Кирхгофа

,

откуда

.

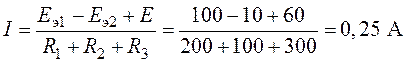4. Показание вольтметра  установленного в схеме будет соответствовать напряжению  на сопротивлении :

.

Задача 7.2.

Методом узловых потенциалов определить токи в ветвях с сопротивлениями  и  схемы (рис. 7.3) , если , , , , , , .

      

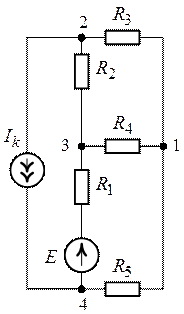
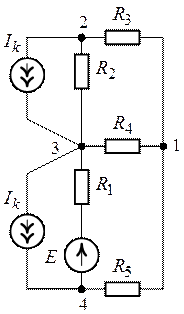
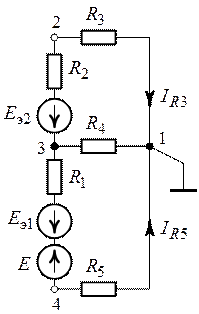
Рис. 7.3.                       Рис. 7.4.                        Рис. 7.5.

Решение.

1. Чтобы уменьшить число узлов расчетной схемы и упростить расчет преобразуем источник тока  в эквивалентные источники ЭДС.

Включая в узле 3 два равных и противоположно направленных источника тока , получим эквивалентную схему (рис. 7.4).

После преобразования источников тока в эквивалентные источники ЭДС получим эквивалентную схеме (рис.7.3) схему представленную на рис. 7.5.

2. Значения ЭДС эквивалентных источников:

;  .

3. Расчет токов преобразованной схемы (рис. 7.5) выполним методом двух узлов. Потенциал узловой точки 1 принимаем равным нулю (). Напряжение между узлами 3 и 1 найдем как

.

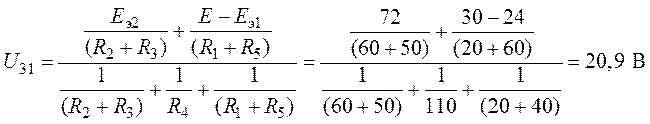4. Интересующие в схеме токи

,

.

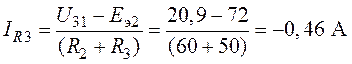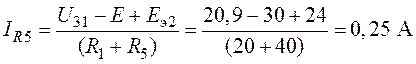Задача 7.3.

Определить показание амперметра для схемы рис. 7.6, если   , , , , , , , , , .

  

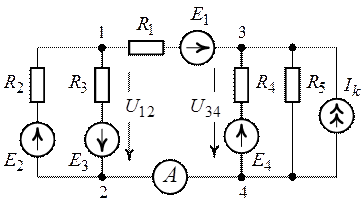
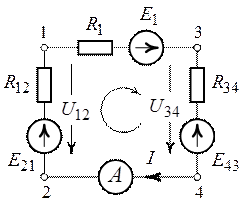
Рис. 7.6.                                         Рис. 7.7.

Решение.

1. Для упрощения расчета воспользуемся преобразованиями активных участков схем с параллельными ветвями одной эквивалентной.

2. Эквивалентная ЭДС  и эквивалентное сопротивление  двух параллельных ветвей левой части схемы (рис. 7.6):