Метод эквивалентного генератора (эквивалентного источника). Применение математической программной среды MathCAD для расчета линейных цепей постоянного тока (главы 6-10 учебного пособия "Теоретические основы электротехники в примерах и задачах"), страница 3

Ваттметр покажет мощность:

.

4. Показание ваттметра, включенного по схеме (рис. 8.4,б). Напряжение, приложенное к измерительной обмотке, найдем по второму закону Кирхгофа для указанного на схеме рис. 8.4,б контура:

,

откуда

.

Ваттметр покажет мощность:

.

5. Показание ваттметра, включенного по схеме (рис. 8.4, в). Напряжение, приложенное к измерительной обмотке

,

откуда

.

Ваттметр покажет мощность:

.

6. Показание ваттметра, включенного по схеме (рис. 8.4, г). Напряжение, приложенное к измерительной обмотке

,

откуда

.

Ваттметр покажет мощность:

.

Задача 8.4.

Для цепи (рис. 8.5) определить ток в линейном резисторе  при условии потребления в нем максимальной мощности, определить максимально возможную мощность  и построить зависимость  . Известно: , , , , , , , .

    

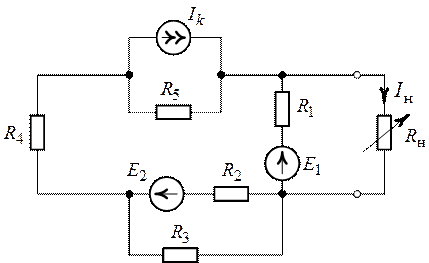
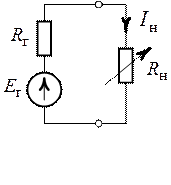
                          Рис. 8.5.                                                  Рис. 8.6.

Решение.

1. Применим теорему об эквивалентном генераторе к схеме рис. 8.5 и рассчитаем ток  в указанной ветви в соответствии с приведенной схемой (рис. 8.6)

.

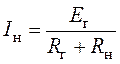2. Найдем ЭДС генератора.  Разомкнем ветвь с сопротивлением  (рис. 8.7) и определим напряжение между точками 1 и 2 ().

  

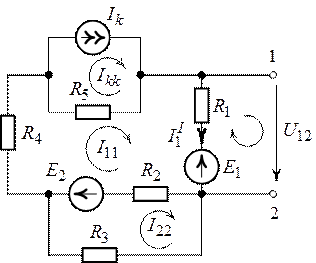
Рис. 8.7.                                            Рис. 8.8.

Расчет цепи (рис. 8.7) выполним по методу контурных токов.  Достаточное количество уравнений равно двум

.

Система контурных уравнений будет иметь вид:

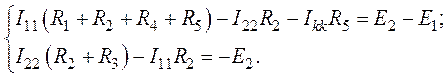
Подставим в систему уравнений числовые значения

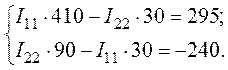
Решение системы позволяет получить

,  .

Действительное значение интересующего тока .

На основании второго закона Кирхгофа найдем напряжение  (рис. 8.7):

,

откуда  .

3. Найдем сопротивление  генератора равное сопротивлению цепи относительно зажимов 1, 2 разомкнутой ветви с сопротивлением   (рис. 8.8).

 

.

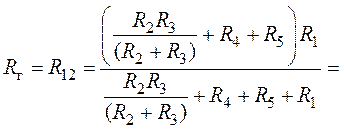
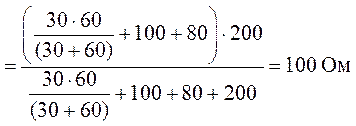4. Найдем сопротивление нагрузки. Максимальная мощность выделится в случае, если сопротивление нагрузки  , т.е.  . Данное утверждение следует из условия выделения максимальной мощности в нагрузке.

5. Найдем ток  в нагрузке для случая :

.

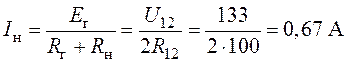6. Максимально возможная мощность, которая выделится в нагрузке, составит:

.

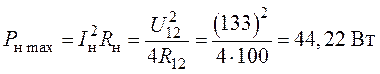7. Построим функциональную зависимость . Мощность, выделяемая в нагрузке при изменении нагрузочного сопротивления будет определяться выражением:

.

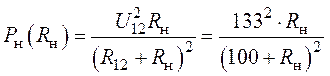Результирующая зависимость  при изменении сопротивления нагрузки в установленных пределах  приведена на рис. 8.9.

Рис. 8.9.

Задача 8.5.

К выходным зажимам двухпроводной линии подключена нагрузка сопротивлением, получающая питание от источника энергии с ЭДС  и внутренним сопротивлением  по схеме рис. 8.10. Определить КПД системы передачи электрической энергии от источника в нагрузку при условии выделения в нагрузочном сопротивлении максимальной мощности, если , сопротивление линии передачи .

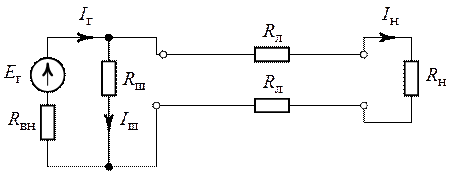
Рис. 8.10.

Решение.

1. Определим ток , проходящий через сопротивление нагрузки

.

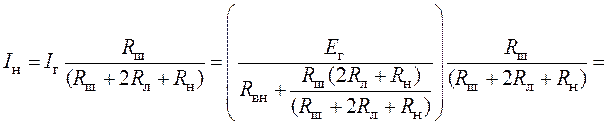
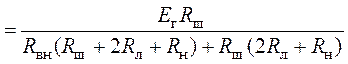2. Рассчитаем выделяемую в сопротивлении нагрузки мощность

.

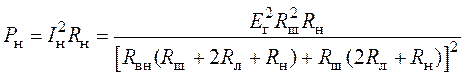3. Определим  при условии выделения в нагрузке максимальной мощности. Для расчета  возьмем производную от   по  и приравняем ее нулю

,

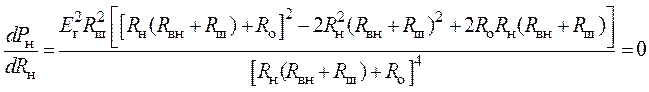где  .

Из условия

получим:

.

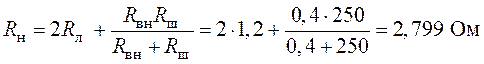Как известно, в схеме, эквивалентной заданной (рис. 8.10) максимальная мощность выделится, если сопротивление нагрузки  будет равно входному сопротивлению цепи относительно зажимов разомкнутой нагрузки и при закороченном источнике ЭДС.

Согласно схеме рис. 8.10 можно определить:

.

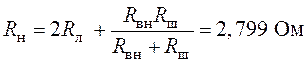Следовательно, получено то же значение , но более простым способом исходя из условия выделения максимальной мощности в нагрузке.

4. Подставляя найденное значение  в выражение для мощности, получим значение максимальной мощности, которая выделится в нагрузке

.

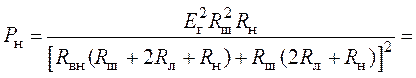
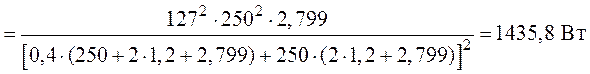5. Вычислим мощность, доставляемую источником ЭДС в схему

.

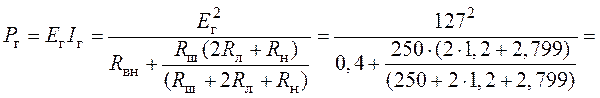
6. КПД системы передачи электрической энергии:

.

Задачи для самостоятельного решения

Задача 8.5. Определить мощность, доставляемую источником тока в схеме (рис. 8.11), если , , , , ,

О т в е т: .

        

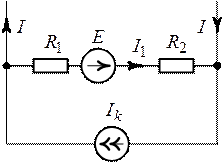
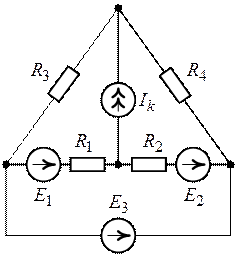
Рис. 8.11.                                             Рис. 8.12.

Задача 8.6. Для цепи (рис. 8.12) определить режим работы источников и проверить выполнение баланса мощности, если  , , , , , , , .

О т в е т:  – генераторный режим;  – режим приемника;  – генераторный режим;  – режим приемника;  мощность всей цепи: .

Задача 8.7. Требуется определить показания ваттметров включенных по схеме, рис. 8.13, если , , .

О т в е т: , , .

Задача 8.8. Определить резистивное сопротивление нагрузки  в схеме, рис. 8.14, при котором в нагрузке выделяется максимально возможная мощность. Определить величину этой мощности. Дано: , , , , , , .

О т в е т: ,  .

         

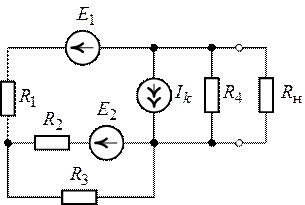
Рис. 8.13.                                             Рис. 8.14.

Задача 8.9. Определить показание ваттметра включенного по схеме, рис. 8.15, если , , , , , , , , , .

О т в е т: .

Задача 8.10. Для цепи (рис. 8.16) проверить выполнение баланса мощности, если , , , , , , .

О т в е т: .

         

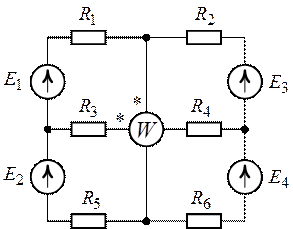
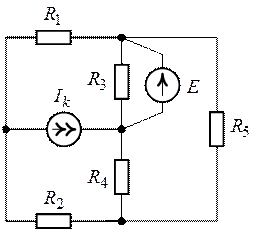
Рис. 8.15.                                             Рис. 8.16.

9. РАСЧЕТ ЭЛЕКТРОСТАТИЧЕСКИХ ЦЕПЕЙ

Расчет электростатических цепей с емкостью на постоянном токе в установившемся режиме сводится к определению напряжений и зарядов отдельных конденсаторов. Особенностью работы цепи с идеальной емкостью на постоянном токе является то, что в установившемся режиме токи через конденсатор не протекают.

Задача 9.1.

Конденсаторы соединены по  схеме (рис. 9.1) и подключены к источнику постоянного напряжения . Определить общую емкость цепи относительно зажимов с источником, заряд и напряжение каждого конденсатора, если , , , .

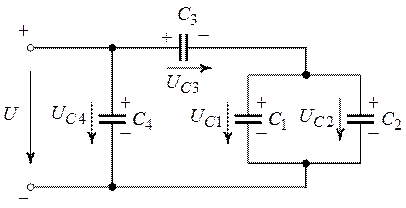
Рис. 9.1.

Решение.

1. Определяя общую емкость, воспользуемся методом свертывания цепи. Конденсаторы  и  включены параллельно. Их общая емкость равна

.

Конденсаторы  и  включены последовательно

.

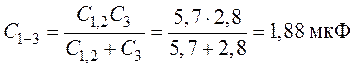Конденсаторы  и  включены параллельно. Общая емкость цепи равна

.

2. Заряды в параллельных ветвях распределятся пропорционально емкостям отдельных ветвей. Заряд  конденсатора :

.

Заряд группы конденсаторов :

.

Заряд  создает напряжения:

,

.

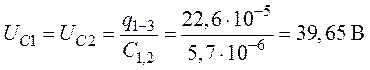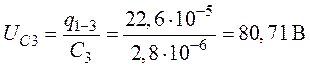Заряды конденсаторов ,  и  распределятся

,

,

.

Задача 9.2.

Для схемы,  изображенной на  рис. 9.2  требуется определить   заряды  и  напряжения  на  конденсаторах, если ,  , , , .

             

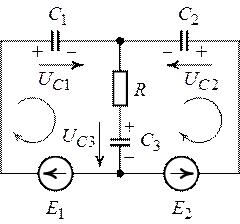
Рис. 9.2.                                             Рис. 9.3.

Решение.

1. На основании электростатической аналогии получим зависимости, аналогичные законам Кирхгофа путем замены токов  на заряды  и проводимостей  на емкости .

Цепь (рис. 9.2) содержит три ветви с емкостью (), два узла  (). Зададим произвольно направления напряжений на конденсаторах (рис.9.3).