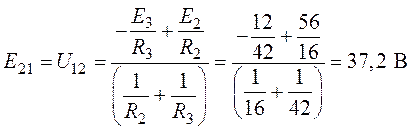Метод эквивалентного генератора (эквивалентного источника). Применение математической программной среды MathCAD для расчета линейных цепей постоянного тока (главы 6-10 учебного пособия "Теоретические основы электротехники в примерах и задачах"), страница 2

,

.

2. Эквивалентная ЭДС  и эквивалентное сопротивление  трех параллельных ветвей правой части схемы (рис. 7.6)

,

.

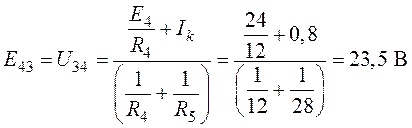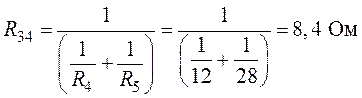4. В результате выполненных преобразований получаем эквивалентную схему, приведенную на рис. 7.7. Показание амперметра определим, составив выражение по второму закону Кирхгофа для обозначенного в схеме (рис. 7.7) контура:

,

откуда определим показания амперметра

.

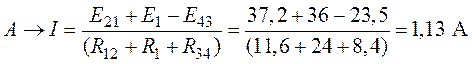Задача 7.4.

Для схемы рис. 7.8, используя метод узловых потенциалов, определить все токи. Дано , , , , , .

    

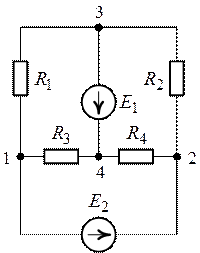
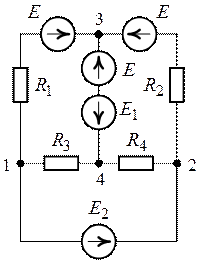
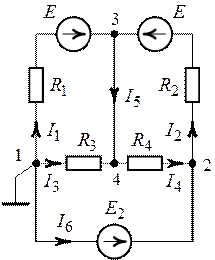
Рис. 7.8.                          Рис. 7.9.                     Рис. 7.10.

Решение.

1. Применение метода узловых потенциалов к расчетной схеме рис. 7.8 затруднительно, т.к. две ветви с источниками ЭДС имеют бесконечно большую проводимость. Указанное затруднение можно легко обойти, если вынести одну из ЭДС за узел и преобразовать цепь.

2. Вынесем ЭДС  за узел 3. Для этого в ветвь с источником ЭДС  внесем ЭДС  равную по значению и противоположную по направлению , а в оставшиеся ветви примыкающие к узлу 3 внесем дополнительные ЭДС  направленные к этому узлу (рис.7.9).

Это не окажет влияния на распределение токов в схеме т.к. внесенные ЭДС взаимно компенсируются.

В ветви с источниками ЭДС, включенной между узлами 3 и 4, действуют одинаковые по значению и противоположно направленные ЭДС, их сумма равна нулю. Поэтому узлы 3 и 4 имеют одинаковый потенциал и их можно закоротить и объединить (рис. 7.10).

3. Примем потенциал узла 1 (рис. 7.10) равным нулю (), тогда потенциал узла 2 равен  () и следовательно по методу узловых потенциалов достаточно составить только одно уравнение для потенциала ранее объединенного узла 3:

.

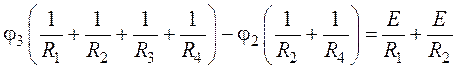4. Решение уравнения позволяет определить неизвестный потенциал узла 3:

.

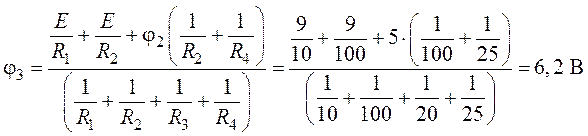Следовательно: , , .

5. В соответствии с заданными направлениями токов в ветвях схемы рис. 7.10 получим:

,

,

,

.

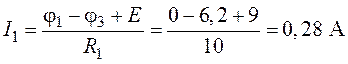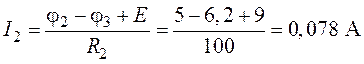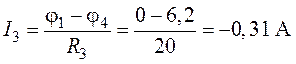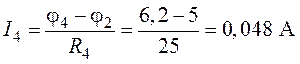Токи  и  в ветвях схемы с источниками ЭДС найдем составив уравнения по первому закону Кирхгофа для узлов 3 и 2:

,

.

Задачи для самостоятельного решения

Задача 7.5. Определить показание амперметра установленного в схеме (рис. 7.11), выполнив предварительно преобразование источников тока в источники ЭДС. Дано , , , , , .

О т в е т: .

Задача 7.6. Для схемы рис. 7.12 определить показание вольтметра, выполнив предварительно преобразования источников тока в источники ЭДС, если , , , , , .

О т в е т: .

          

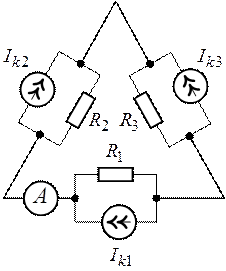
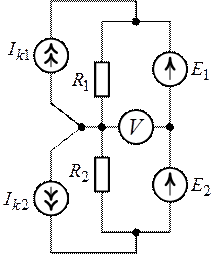
Рис. 7.11.                                             Рис. 7.12.

Задача 7.7. Для схемы рис. 7.13 определить показание амперметра, если , , , , , , . Решение выполнить преобразованием группы из трех параллельно соединенных ветвей с источниками ЭДС одной эквивалентной.

О т в е т: .

Задача 7.8. Методом узловых потенциалов определить все токи в ветвях схемы рис. 7.14, если , , , , , .

О т в е т: , , , ,

, .

            

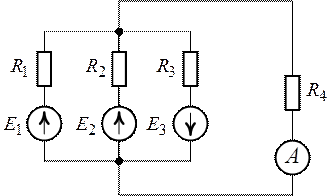
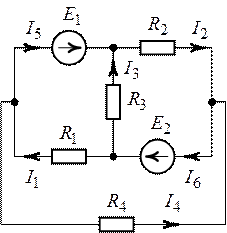
Рис. 7.13.                                           Рис. 7.14.

8. ЭНЕРГЕТИЧЕСКИЕ РАСЧЕТЫ В ЦЕПЯХ

ПОСТОЯННОГО ТОКА

При выполнении энергетических расчетов в электрических цепях постоянного тока интересуют характеристики связанные с определением мощности рассеиваемой в сопротивлениях резисторов, условий потребления максимальной мощности в нагрузке, мощности источников напряжения и тока и режимов их работы, баланса мощностей, к.п.д. передачи энергии.

Задача 8.1.

Для цепи (рис.8.1) требуется определить режим работы каждого источника и установить баланс мощностей, если , , , , , , .

Решение.

1. Выполним расчет токов в ветвях схемы по методу узловых потенциалов. Схема (рис. 8.1) содержит пять ветвей (), из которых четыре с неизвестными токами, три узла (), одна ветвь с нулевым сопротивлением содержит источник –  ().

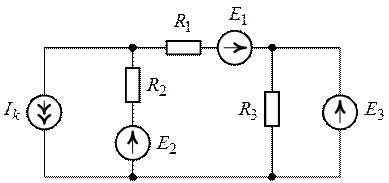
Рис. 8.1.

2. Общее число расчетных уравнений равно одному

.

Потенциал узловой точки 1 (рис. 8.2) примем равным нулю (). Тогда потенциал узловой точки 3 (рис.8.2) равен  ().

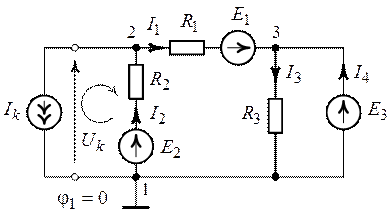
Рис. 8.2.

3. Потенциал узловой точки 2 найдем на основании уравнения, составленного для :

.

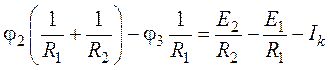4. Решением уравнения относительно неизвестного потенциала с учетом того, что  будет

.

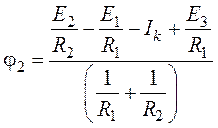
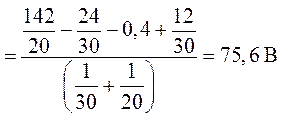5. Зададим положительное направление токов в ветвях схемы , как указано на рис. 8.2.  По закону Ома выразим токи:

;

;

.

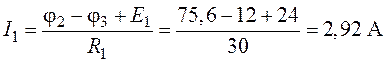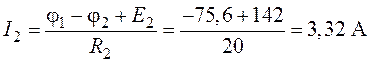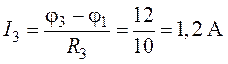По первому закону Кирхгофа для узла 3 найдем  

.

6. Определяем режимы работы источников энергии.  Отрицательный знак для тока  означает, что действительное направление тока противоположно указанному на схеме (рис. 8.2). Из этого следует, что источник  работает в режиме приемника (потребителя) электрической энергии.  Его мощность

.

Источники   и  генерируют  электрическую энергию в цепь, т.к. действительное направление тока совпадает с направлением источников:

;

.

Мощность источника тока

.

Напряжение  на зажимах источника тока также можно  было принять равным напряжению узловой точки 2, т.е. .

Отрицательный знак мощности означает, что источник тока работает в режиме приемника (потребителя) электрической энергии.

7. Уравнение баланса мощностей

.

После подстановки в уравнение числовых значений получим:

;

.

Результаты расчета показывают, что баланс мощностей выполняется.  Ошибка при расчетах составляет.

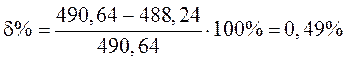
Задача 8.2.

Для схемы (рис. 8.3) определить показание ваттметра и убедиться в том, что оно равно сумме мощностей, расходуемых во всех резистивных сопротивлениях, если , , , , , .

Решение

1. Выполним расчет всех токов в ветвях схемы. Расчеты целесообразно выполнить по методу узловых потенциалов.

Потенциал узловой точки 1 (рис. 8.3) примем равным нулю (). Тогда потенциал узловой точки 3 равен , т.е. напряжению на входе цепи ().

Рис. 8.3.

2. Расчетные уравнения для определения потенциалов  и  будут иметь вид:

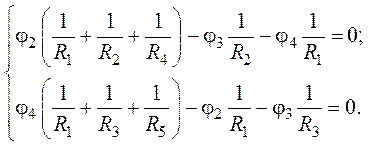
3. После подстановки числовых значений получим:

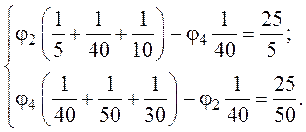
Откуда , .

4. Находим токи в ветвях схемы:

;

;

;

;

.

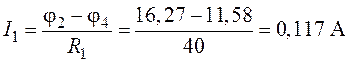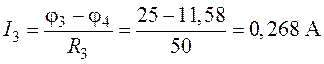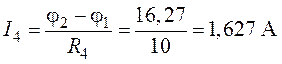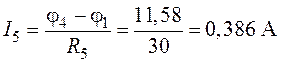Ток на входе цепи  .

5. Показание ваттметра

,

где .

6. Суммарная мощность, расходуемая во всех резистивных сопротивлениях:

.

.

На основании выполненных расчетов следует тождество:

Погрешность при выполнении баланса вызвана заданной перед расчетом точностью определения токов в расчетной схеме.

Задача 8.3.

Для цепи (рис. 8.4) требуется определить показания ваттметра для различных схем включения измерительных обмоток. Дано: , , , , , , .

      

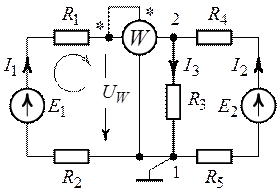
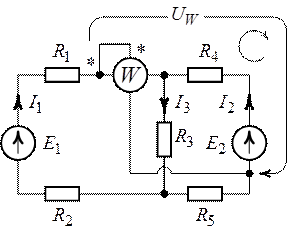
а                                                                   б

      

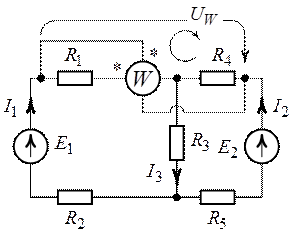
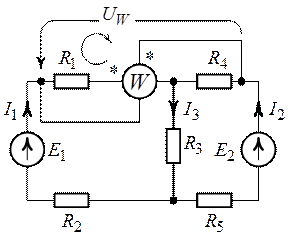
в                                                                   г

Рис. 8.4.

Решение.

1. Выполним расчет токов в ветвях схемы по методу двух узлов. Потенциал узловой точки 1 примем равным нулю ().  Напряжение между узловыми точками 2 и 1 (рис. 8.4, а)

.

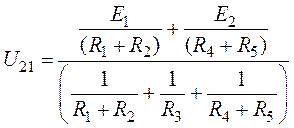
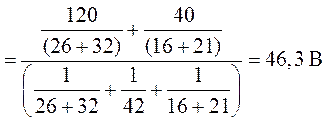2. Токи в ветвях  цепи:

;

.

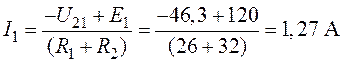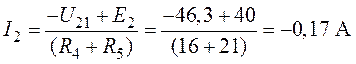3. Показание ваттметра включенного по схеме (рис. 8.4, а). Напряжение, приложенное к измерительной обмотке, .