Метод эквивалентного генератора (эквивалентного источника). Применение математической программной среды MathCAD для расчета линейных цепей постоянного тока (главы 6-10 учебного пособия "Теоретические основы электротехники в примерах и задачах"), страница 4

2. Определим достаточное  количество уравнений для расчета цепи по законам Кирхгофа.

По первому закону Кирхгофа для зарядов:

.

По второму закону Кирхгофа для напряжений:

.

Положительное направление обхода контуров определим в соответствии с заданными на рис. 9.3.

3. Система уравнений по законам Кирхгофа с учетом, что  т.к. токи по контурам не протекают

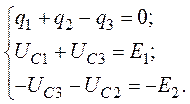
Полагая, что 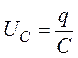 представим систему в виде:

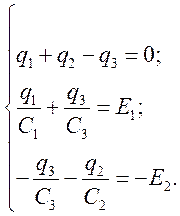
4. Решение системы получим в матричной форме:

.

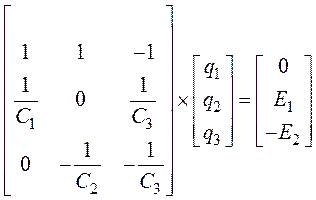5. После подстановки числовых значений получим

.

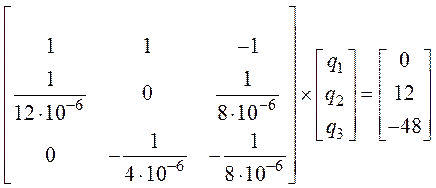6. Решение матричной системы позволяет определить заряды конденсаторов

,   ,   .

Отрицательный знак заряда  указывает на противоположную указанной на рис. 9.3 полярность заряда .

7. Напряжения на конденсаторах

,

,

.

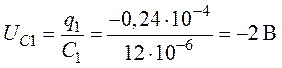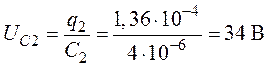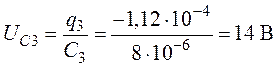8. Проверка решения, в соответствии  с которой алгебраическая сумма зарядов на обкладках конденсаторов, присоединенных к узлу  (рис. 9.3), должна быть равна нулю:

.

Задача 9.3.

Определить напряжение каждого конденсатора и энергию  электрического поля всей цепи (рис. 9.4).  Дано ,  , , , , , , , .

   

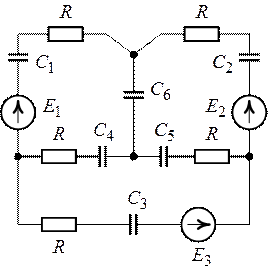
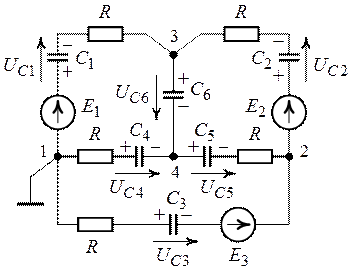
Рис. 9.4.                                               Рис. 9.5.

Решение.

1. Расчет электрической цепи (рис. 9.4) целесообразно выполнить методом узловых потенциалов.

Цепь (рис. 9.4) содержит шесть ветвей, каждая из которых включает в себя емкостной элемент (), четыре узла ().

Зададим произвольно положительное направление напряжений на конденсаторах (рис. 9.5).

2. Достаточное количество уравнений для расчета цепи по методу узловых потенциалов равно трем:

.

Обозначение узлов в схеме выполним в соответствии с рис. 9.5. Потенциал узла 1 примем равным нулю ().

3. Расчетные уравнения для определения потенциалов ,  и  (узлы 2, 3 и 4) на основании формальной аналогии между электрическими и электростатическими цепями, будут иметь вид:

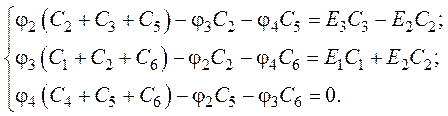
4. Для расчета приведем систему к матричной форме

.

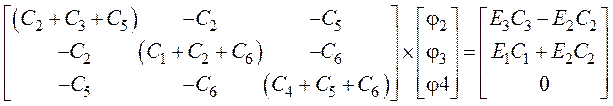5. После подстановки в систему числовых значений и решения матричной системы найдем

,  ,  .

6. С учетом заданных положительных направлений напряжений на конденсаторах (рис. 9.5) получим

,

,

,

,

,

.

7. Энергия электрического поля всей цепи будет составлять сумму энергий электрического поля каждого конденсатора

.

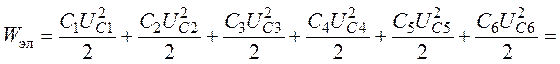
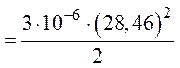
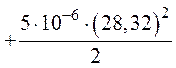
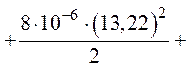
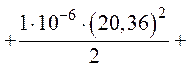
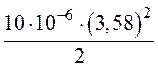
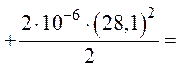
8. Проверим правильность решения. По второму закону Кирхгофа для внешнего контура цепи (рис. 9.5) запишем:

.

После подстановки числовых значений получим:

,

.

Задачи для самостоятельного решения

Задача 9.4. Для схемы (рис. 9.6) определить общую емкость конденсаторов, заряд и напряжение каждого конденсатора, если  , , ,  , , .

О т в е т: , , ,

 , , ,

, , .

Задача 9.5. Для схемы (рис. 9.7) определить общую емкость цепи относительно входных зажимов источника ЭДС и энергию, запасаемую в электрическом поле всей цепи. Дано: , , , , , , .

О т в е т: ,  .

      

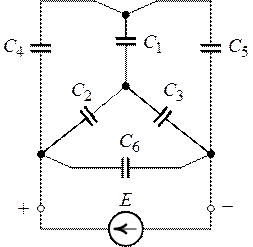
Рис. 9.6.                                                     Рис. 9.7.

Задача 9.6. Для схемы (рис. 9.8) требуется определить заряд, напряжение  каждого  конденсатора и энергию электрического поля всей цепи, если , , , , , .

О т в е т: , , , , , , ,

,  .

Задача 9.7. Конденсаторы соединены по схеме, как на рис. 9.9. Определить напряжение, приложенное к каждому конденсатору, если , , , , , , .

О т в е т: , , , , .

               

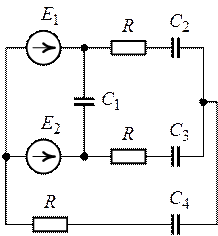
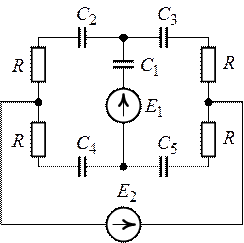
Рис. 9.8.                                          Рис. 9.9.

Задача 9.8. Определить заряды на конденсаторах включенных по схеме рис. 9.10, если , , ,  , , , .

О т в е т: , , , .

Задача 9.9. Найти заряд конденсатора включенного по схеме рис. 9.11. Дано: , , , , , .

О т в е т: .

   

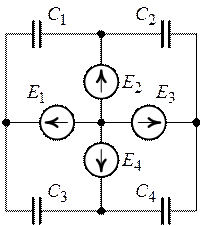
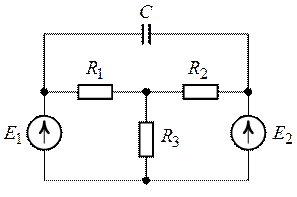
Рис. 9.10.                                          Рис. 9.11.

10. ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОЙ

ПРОГРАММНОЙ СРЕДЫ  MATHCADДЛЯ

РАСЧЕТА ЛИНЕЙНЫХ ЦЕПЕЙ ПОСТОЯННОГО

ТОКА

При расчете электрических цепей возникает задача решения систем алгебраических уравнений. C целью автоматизации и ускорения процесса расчета рассмотрим основные приемы решений систем линейных алгебраических уравнений, описывающих состояние цепей, с помощью математической программной среды MatCAD.

Покажем основные возможности этой среды для решения практических задач.

Задача 10.1.

Определить токи в ветвях цепи (рис. 10.1) методом непосредственного применения законов Кирхгофа, если , , , , , , , .

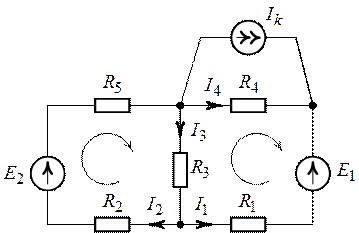
Рис. 10.1.

Решение.

1. Система уравнений, составленная по законам Кирхгофа для расчета цепи (рис. 10.1) имеет вид:

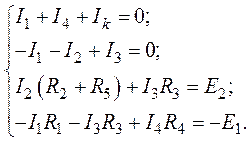
2. Приведем систему к матричной форме записи:

.

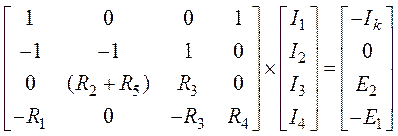3. После подстановки числовых значений получим

.

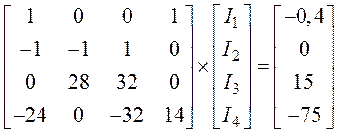4.Решение матричной системы позволяет определить токи ветвей:

,  ,  ,  .

5. Решение системы линейных алгебраических уравнений в  MathCAD различными способами:

Способ 1. С помощью определителей по формулам Крамера.

Пример вычислительного блока реализованного в среде MathCAD:

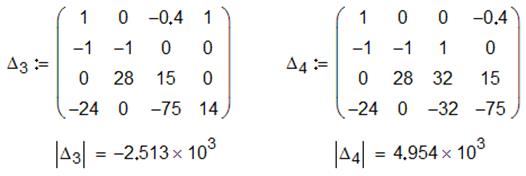
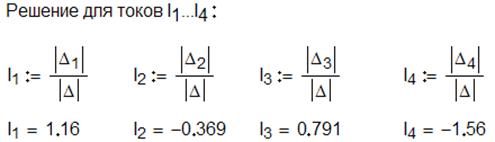
Способ 2. С помощью векторных и матричных операторов при решении задач линейной алгебры.

Пример вычислительного блока реализованного в среде MathCAD:

Способ 3. Решение матричной системы с применением функции  .

Пример вычислительного блока реализованного в среде MathCAD:

Решение матричной системы с применением функции   в ином формате:

Способ 4. Решение системы уравнений при помощи вычислительного блока «».

Пример вычислительного блока реализованного в среде MathCAD:

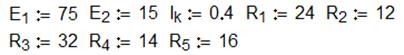
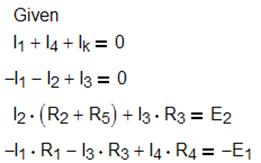
П р и м е ч а н и е:  В качестве знака равенства в системе линейных уравнений следует использовать знак логического равенства панели  .

Задача 10.2.

Определить токи в ветвях схемы (рис. 10.2) методом узловых потенциалов. Дано , , , , , , , .

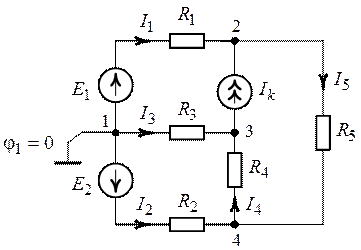
Рис. 10.2.

Решение.

1. Примем потенциал узловой точки 1, равным нулю (). Система расчетных уравнений для определения потенциалов  ,  и  будет иметь вид:

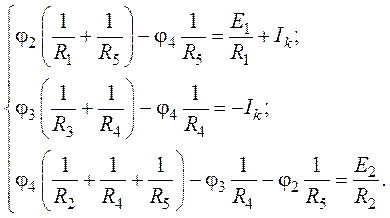
2. Приведем систему к матричной форме записи

.

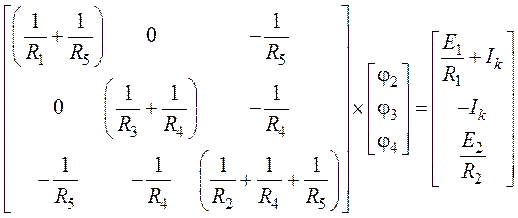3. Решение матричной системы получим в MathCAD при помощи векторных и матричных операторов.

Пример вычислительного блока реализованного в среде MathCAD:

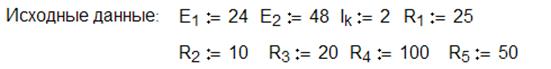
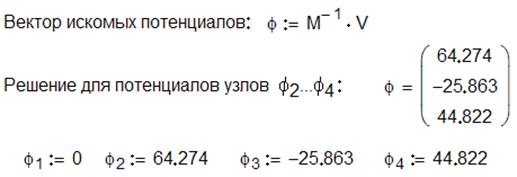
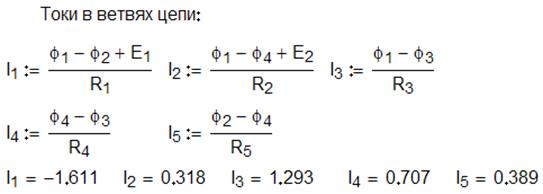
В результате решения получены токи: , , , , .

Задача 10.3.

Пользуясь методом контурных токов рассчитать все токи в ветвях схемы (рис. 10.3), если , , , , , , , , , , , , .

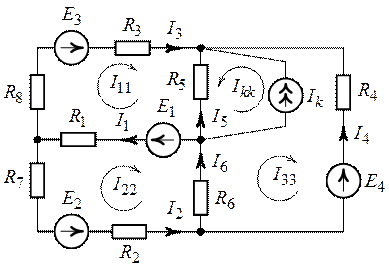
Рис. 10.3.

Решение.

1. Система уравнений, составленная по второму закону Кирхгофа относительно контурных токов имеет вид:

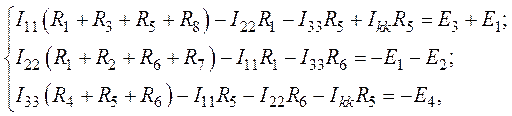
где  .

2. Действительные токи в ветвях цепи определяться как алгебраическая сумма контурных токов смежных контуров:

  ,  ,  ,

,  .

3. Решение системы линейных уравнений и расчет действительных токов в ветвях схемы получим в MathCAD при помощи вычислительного блока «»

Пример вычислительного блока реализованного в среде MathCAD:

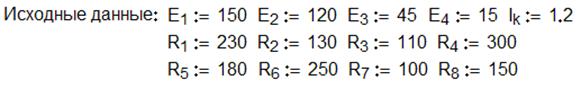
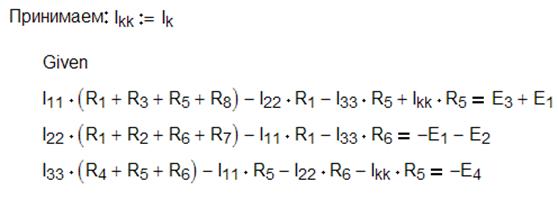
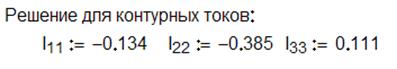
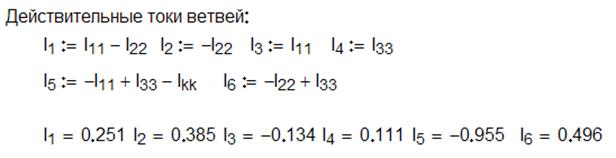
В результате решения в  MathCAD с помощью вычислительного блока «» получены следующие значения токов:

, , ,

, , .