Теоретические основы электротехники. Электротехника: Контрольные задания с методическими указаниями, страница 6

При составлении уравнений по второму закону Кирхгофа знак напряжения взаимной индукции   на элементе n, вызванное током, протекающим в элементе s , определяется на основании сопоставления обхода элемента n и положительного направления тока в элементе s .  Если эти направления относительно одноименных зажимов одинаковы, то напряжения взаимной индукции  берется со знаком плюс (+):

.

В противном случае, напряжение взаимной индукции берется со знаком минус  .

В данной задаче .

Расчетные уравнения, составленные на основании законов Кирхгофа для выбранного направления токов,  имеют вид:

для узла b:   ;

для контура :

 ;

для контура : .

Решение системы уравнений дает значения токов, , .

б)  С учетом «развязи» индуктивных связей

Правило «развязки» магнитных (индуктивных) связей:  при устранении индуктивной связи к сопротивлению   и   добавляется сопротивление , зажим 3 (b) перестает быть узлом для ветвей 1 и 2, и между зажимом 3(b) и новым узлом (d) появляется элемент  .  Верхние знаки берутся для случая, когда индуктивно связанные  элементы подключены к узлу 3 () одноименными зажимами (см. рис. 6.4).

Применяя правило «развязки» магнитных связей, переходим от схемы, изображенной на рис. 6.3, к эквивалентной  схеме, изображенной на рис. 6.5.

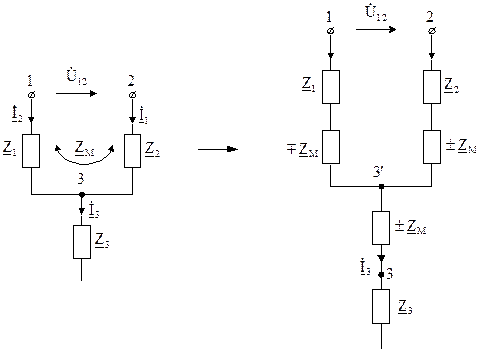
Рис. 6.4

j xL1

j xм

j xC1

j xм

j xL2

– j xм

n

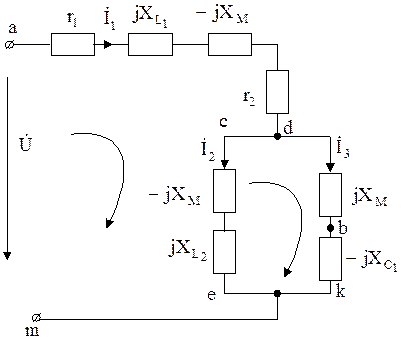
Рис. 6.5

Расчетные уравнения, составленные на основании законов Кирхгофа, для схемы рис. 6.5 имеют вид:

для узла b:  ;

для контура :

 ;

для контура : .

Решение системы уравнений дает             значения токов , , .

Задача 3

xC2

x

x

x

x

x

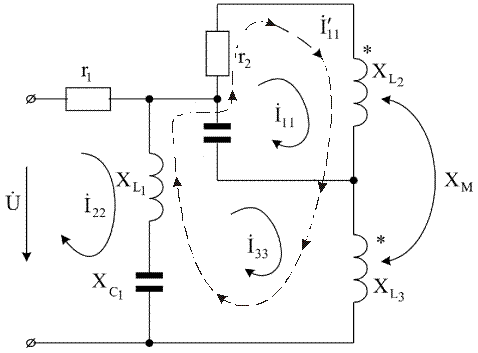
Рис. 6.6

Для цепи, изображенной на рис. 6.6, сформировать систему алгебраических уравнений по методу контурных токов.

В методе контурных токов сравниваются направления контурных токов относительно одноименных зажимов двух индуктивно связанных элементов цепи. Если контурные токи относительно одноименных зажимов элементов k и s  протекают согласно, то соответствующее сопротивление взаимной индукции    берется со знаком «плюс» и наоборот.

В соответствии с выбранными положительными направлениями контурных токов система уравнений имеет вид:

а)  вариант с контурными токами  , , :

 ,  (*)

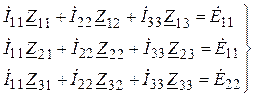где                            ;

;

=

,   ,  

б)  вариант с контурными токами  , , :

общий вид выражения (*)  сохраняется, но сопротивления, входящие в систему, имеют другие значения (вместо тока   надо подставить ):

;

Основные правила  работы

с комплексными числами

Из курса математики известно, что любая точка на комплексной плоскости  может быть представлена комплексным числом, записанным в алгебраической форме   или показательной форме  .

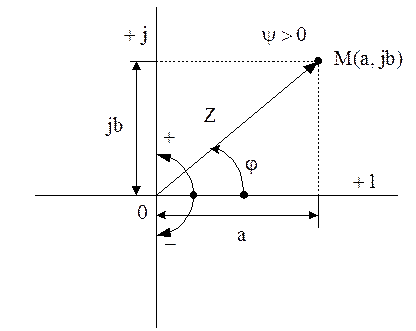
Рис. 6.7

Из рисунка видно, что алгебраическая и показательная формы связаны соотношениями: 

=,

где  – модуль комплексного   числа,

  – аргумент;  ;   .

При работе с комплексными числами необходимо помнить, что сложение и вычитание удобно производить в алгебраической форме,  а умножение  и деление  в показательной  (полярной) форме.

Соотношения, необходимые при работе с комплексными числами:

а) ,

б) ,

в)

г)

д)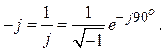

Связь между показательной и полярной формой записи: ,  .

Контрольные примеры работы с комплексными числами

Перевод из алгебраической формы в показательную (полярную):

а)