Теоретические основы электротехники. Электротехника: Контрольные задания с методическими указаниями, страница 3

6.  Построить потенциальную диаграмму для внешнего контура цепи.

Параметры  схемы (рис. 5.1):

 В,  В,

 А,

Ом, Ом, Ом, Ом, Ом, Ом.

1. Расчет цепи методом токов  ветвей

(непосредственное применение законов Кирхгофа)

1.1. Выберем положительные направления токов в ветвях, как это указано на рис. 5.2.

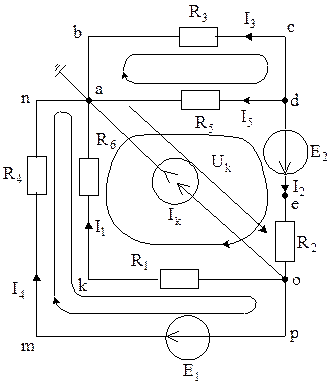
Рис. 5.2

1.2. Определяем количество уравнений, которые должны быть составлены по законам Кирхгофа:

а) число уравнений, составляемых по первому закону Кирхгофа, равно:

=,  где  – число узлов в схеме;

б) число  уравнений, составляемых по второму закону Кирхгофа, равно:

,

где – число ветвей схемы,  – число источников тока.

Таким  образом, общее число независимых уравнений, составленных по законам Кирхгофа, равно числу неизвестных токов в пяти ветвях схемы.  Для ветви с источником тока ток определен и равен току источника тока. 

1.3. а)  уравнения по первому закону Кирхгофа:

для узла  а: ,

для узла  o: .

б) для записи уравнений по второму закону Кирхгофа независимый контур выбираем так, чтобы он не содержал источников тока.  

Уравнения по второму закону Кирхгофа:

для контура  a k o p m n a:   ,

для контура   a d e o k a:       ,

для контура   a b c d  a:          .

1.4. После подстановки числовых значений в уравнения по п.1.3  получаем систему уравнений

                                      

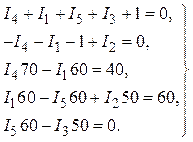
Решение системы уравнений  относительно неизвестных токов   позволяет получить их значения: , , , , .  Отрицательный знак для токов , , , , означает, что истинное направление тока противоположно направлению, выбранному в качестве положительного.

1.5. Проверку сделаем по второму закону Кирхгофа, например, для внешнего контура  a b c d e o p m n a:

,

 В,

 В.

Погрешность в расчетах составляет

2. Расчет по методу контурных токов

2.1. Положительное направление токов  оставляем в соответствии с п.1.1 решаемой задачи 1, как это изображено на рис. 5.2 и 5.3.

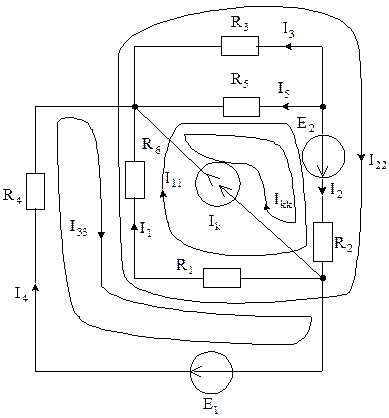
Рис. 5.3

2.2. Количество уравнений равно:

.

2.3. Обратимся к схеме цепи, изображенной на рис. 5.3, и выберем произвольное направление контурных токов, которые обозначим   , , .

Предположим, что  ток источника тока    замыкается по дополнительному  контуру, и будем считать его  известным контурным током, обозначив его  , как это показано на рис. 5.3  ().

Принимая направление обхода контуров совпадающими с направлением контурных токов, составим систему уравнений для контурных токов:

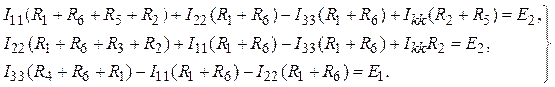Полученную систему преобразуем к следующему виду:

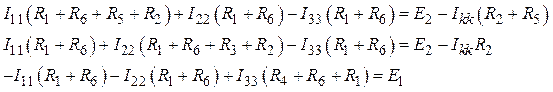
2.4. Решение полученной системы  уравнений будет иметь вид:

,  , ,

где  – определитель системы, , ,   – алгебраические дополнения

=

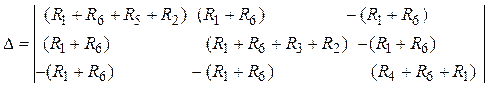(Ом³);

;

.

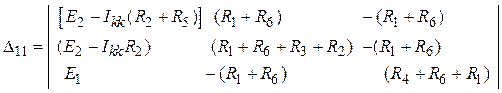Аналогично составляем алгебраическое дополнение .

Сопоставляя положительные направления токов в ветвях, указанных на рис. 5.3, с направлениями найденных контурных токов, истинные токи определим следующим образом:

= А,        = А,

= А,        = А,

= А.

3. Расчет по методу узловых потенциалов

(напряжений)

Расчет цепи  (рис. 5.2) производим  в два этапа.

На первом этапе определяются узловые  потенциалы.

На втором этапе определяются токи в ветвях схемы, используя найденные узловые потенциалы.

3.1. Количество уравнений по методу узловых  потенциалов равно =.

3.2. Принимаем потенциал узла   равным нулю:  (как правило, это узел, где сходится наибольшее количество ветвей).

3.3. Расчетные уравнения для определения потенциалов    и .

,

=.

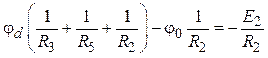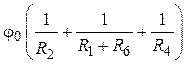
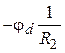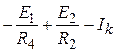3.4. После подстановки числовых значений, имеем:

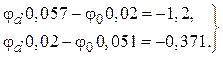
Решение системы относительно неизвестных потенциалов узлов равно:

 В,  В.

3.5. Определение токов. 

По закону Ома для участка цепи с ЭДС в соответствии с рис. 5.2 имеем:

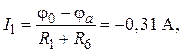
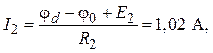
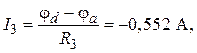
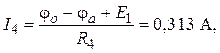
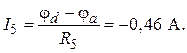
4. Расчет по методу эквивалентного генератора

4.1. Выделим ветвь с сопротивлением , по которой протекает искомый ток . Исходную схему рис. 5.4, а по отношению к зажимам ветви с сопротивлением  представим в виде эквивалентного генератора рис. 5.4, б, ЭДС которого (Е_г) численно равна напряжению холостого хода на зажимах разомкнутой ветви, а внутреннее сопротивление генератора   равно входному сопротивлению цепи относительно выделенных зажимов  ео.