Теоретические основы электротехники. Электротехника: Контрольные задания с методическими указаниями, страница 5

Потенциалы остальных  узлов определяются из уравнений

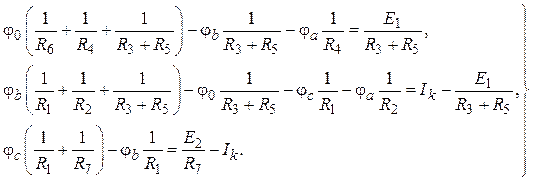
Решение системы уравнений дает значения потенциалов , , .

Задавшись произвольным положительным направлением токов во всех ветвях схемы, по закону Ома для участка цепи с ЭДС получим:

,    ,        ,

,   ,   .

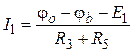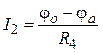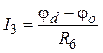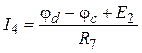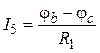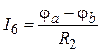Ток в ветви с источником ЭДС  определяют из уравнения, составленного по первому закону Кирхгофа. Например, для узла а:

, откуда .

Напряжение между узлами    и 

.

Задача 4

φа= 0

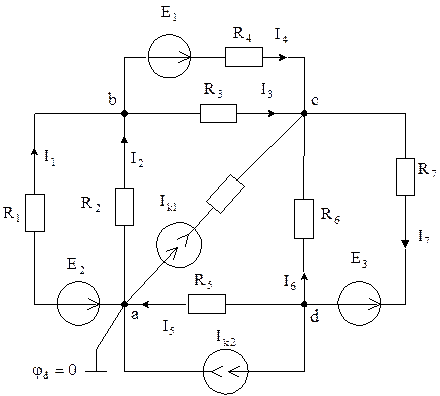
Рис. 5.10

Для схемы цепи, изображенной на рис. 5.10, сформировать систему алгебраических уравнений для расчета токов рациональным методом.  Дать решение в общем виде относительно неизвестных токов. Параметры схемы  , , , ,    заданы.

Количество уравнений:

1.  По законам Кирхгофа

Число уравнений по первому закону равно

.

Число уравнений по второму закону равно

.

Таким образом, при непосредственном применении к расчету   цепи законов Кирхгофа необходимо составить систему из семи алгебраических уравнений.

2.  По методу контурных токов число уравнений равно:

.

3.  По методу узловых потенциалов число уравнений равно:

Таким образом, расчет цепи методом узловых потенциалов  является наиболее рациональным.

Расчетные уравнения для определения потенциалов имеют вид ():

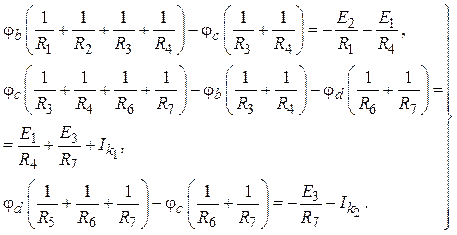
Решение системы дает   значения  , , .

Используя закон Ома для участков цепи с ЭДС, получим:

,   , ,  , ,  ,  .

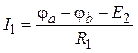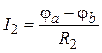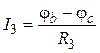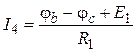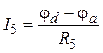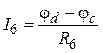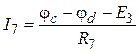6. примеры решения задач по теме

«Расчет линейных электрических цепей

однофазного синусоидального тока»

Задача 1

к

V

xL1

Рис. 6.1

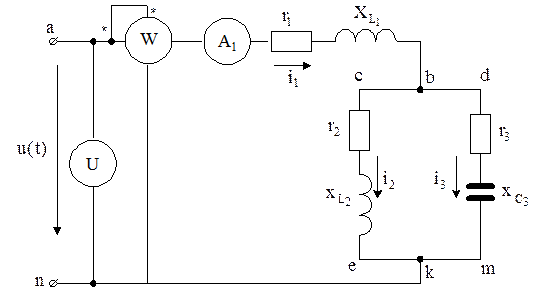
Параметры цепи, схема которой изображена на  рис. 6.1, имеют следующие значения:   Ом,   Ом,  Ом,  Ом,  Ом,  Ом.

Напряжение на зажимах цепи равно:

 В.

Определить токи  , ,  и показания приборов электромагнитной системы. Рассчитать активную, реактивную и полную мощности цепи.

Решение

1.1. Переносим решение задачи в комплексную плоскость (переходим к комплексным действующим значениям величинам).   В.

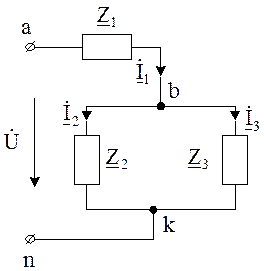
Исходная схема при этом принимает вид, изображенный на рис. 6.2.

к

  

Рис. 6.2

Ом,

=Ом,

Ом,

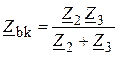
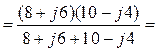
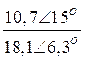Ом,

=Ом.

Комплексное сопротивление цепи относительно зажимов с источником равно:

=+== Ом.

Полное сопротивление цепи равно: Z = 18,8 Ом.

1.2. Комплексы токов  имеют следующие значения:

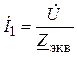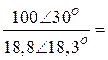
=А,

,   , 

.

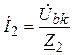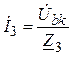Соответственно, числовые значения равны:

=

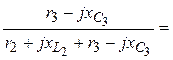
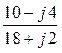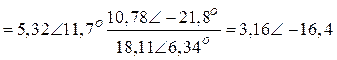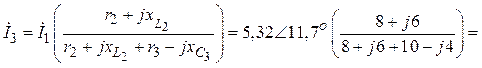
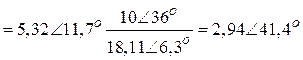 А,

  А,

1.3.  Мгновенные значения токов  равны:

  А,

1.4.  Показание амперметра и вольтметра равны, соответственно, действующим значениям тока и напряжения:

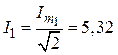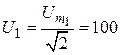  А,             В.

1.5. Расчет активной, реактивной и полной мощности цепи.

Комплексная мощность цепи равна:

===   

=  ВА.

Активная мощность   равна:

=  Вт.

Реактивная мощность  равна

= ВАр.

Полная мощность цепи равна

  ВА

1.6. Показание ваттметра.

Ваттметр, изображенный на рис. 6.1, измеряет активную мощность всей цепи:

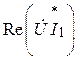
= Вт.

Задача 2

Параметры цепи, схема которой изображена на рис. 6.3, заданы. На основе законов Кирхгофа, сформировать систему  алгебраических уравнений относительно неизвестных комплексов токов:

а) без учета развязки индуктивных связей;

x

б) с учетом развязки индуктивных связей.

x

x

1

n

xм

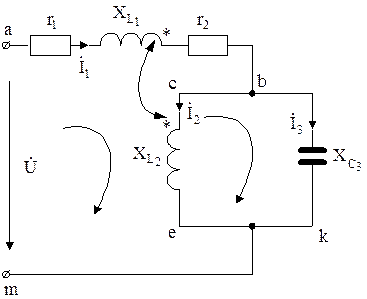
Рис. 6.3

Решение

а)  Без учета развязки индуктивных связей