Теоретические основы электротехники. Электротехника: Контрольные задания с методическими указаниями, страница 2

=,

=,      (4.3)

=,

где   – собственная проводимость узла  , равная сумме проводимостей всех ветвей, присоединенных к  «»-му узлу:

,     ,

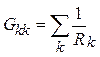 – общая проводимость узлов «k» и «»,  равная сумме проводимостей ветвей, соединяющих узлы «k» и «». Общая проводимость узлов всегда отрицательная:

.

 – алгебраическая сумма произведений ЭДС источников на проводимости тех ветвей, которые присоединены к узлу «» и содержат источники ЭДС.

Произведение  берется со знаком  «плюс» в том случае, если в рассматриваемой ветви ЭДС направлена к узлу «k», и со знаком «минус», когда ЭДС направлена от узла «k» .

 – алгебраическая сумма задающих токов источников тока, связанных с узлом «». Задающие токи , втекающие в узел, берутся со знаком «плюс», а вытекающие из узла – со знаком «минус». Решая систему (4.3) , находят потенциалы всех узлов. Истинные токи рассчитывают по закону Ома для участка цепи с ЭДС:

Для схемы рис. 4.1.  имеем:

 ,      ;

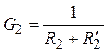 ,      ;                (4.4)

,     

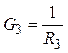
и т.д.   

Частным случаем метода узловых потенциалов является    метод двух узлов, применяемый к схеме, содержащей множество ветвей и всего два узла (рис. 4.2) (параллельное  соединение ветвей, содержащих  ЭДС и  источники токов).          

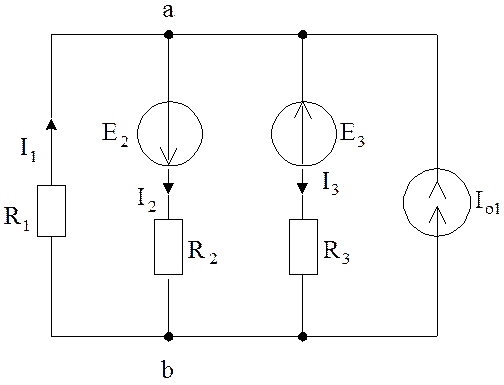
Рис. 4.2

Применим метод узловых  потенциалов к схеме, изображенной на рис. 4.2.

Число уравнений, которые  должны быть составлены согласно методу, равно .  Составим уравнение для узла  а:

,                   (4.5)

где                   =,

                              =,

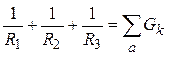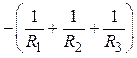,                                     (4.6)

,

.

С учетом соотношения (4.6),  перепишем уравнение (4.5)

=.                  (4.7)

Из уравнения (4.7) имеем:

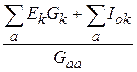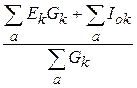==.      (4.8)

Токи равны (см. рис. 4.2)

;  ,                   (4.9)

.

Если в схеме имеются ветви, содержащие идеальные источники ЭДС (проводимости таких ветвей бесконечно велики), то эти  ветви следует рассматривать  как источники неизвестных токов, которые  исключаются  при сложении уравнений, составленных формально по методу узловых потенциалов.  Дополнительными связями между неизвестными узловыми потенциалами будут являться известные напряжения между узлами, равные заданным ЭДС.

При наличии только одной ветви с идеальной ЭДС и бесконечной проводимостью целесообразно принять за базисный узел один из узлов, к которому примыкает данная ветвь; тогда потенциал другого узла становится известным и число неизвестных (число уравнений) сокращается на одно.

Пример. Считаем равным нулю потенциал узла 4 ( – базисный узел, рис. 4.3).

Согласно схеме (рис. 4.3) 

 ,

здесь .

Число неизвестных потенциалов, а следовательно, и уравнений, равно двум (, , ). 

I3

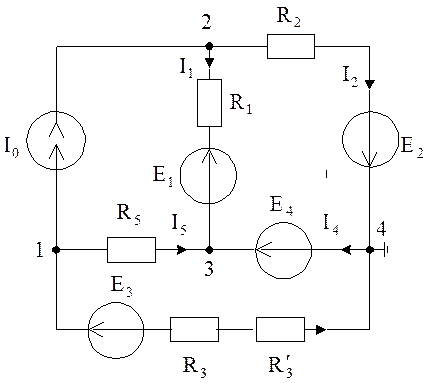
Рис. 4.3

Составим уравнения применительно к узлам, потенциалы которых неизвестны

,                       (4.10)

.

Соответственно:

,      ,   

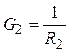 – сопротивление идеального источника  тока равно бесконечности,  соответственно проводимость  ,

,     .

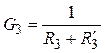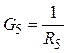Учитывая, что в уравнениях (4.10)   и  , перепишем их в следующем виде:

,

.               (4.11)

Из системы (4.11)  находим значения    и    и токи в ветвях, используя закон Ома для участка цепи с ЭДС:

;

;

;

.                   ( 4.12)

Ток в ветви с идеальным источником ЭДС определяется  по первому закону Кирхгофа:  

узел  3:                       (4.13)

5.  примеры решения задач  к теме

«Линейные электрические цепи постоянного тока»

Задача 1

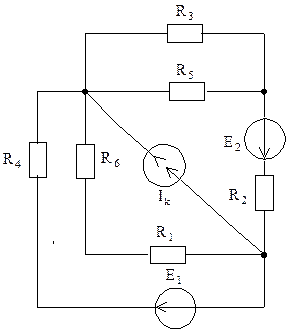
Рис. 5.1

Для схемы электрической цепи, изображенной на рис. 5.1, выполнить  следующее.

1.  Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях исходной схемы и рассчитать эти токи.

2.  Рассчитать токи во всех ветвях методом контурных токов.

3.  Рассчитать токи  во всех ветвях методом    узловых потенциалов.

4.  Определить ток в ветви с сопротивлением , используя метод эквивалентного генератора.

5.  Составить уравнение баланса мощностей и оценить точность проделанного расчета по методу токов ветвей.