Теоретические основы электротехники. Электротехника: Контрольные задания с методическими указаниями, страница 4

а

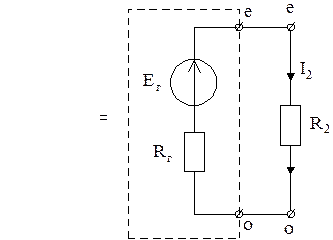
б

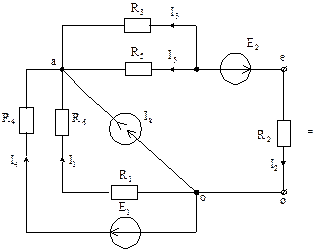
Рис. 5.4

Для вновь образованной схемы (рис. 5.4, б), на основании второго закона Кирхгофа, определим ток в ветви с сопротивлением R₂:

.

Основной расчет сводится  к определению параметров эквивалентного генератора  и  .

4.2. По определению  равно напряжению холостого хода  на зажимах  разомкнутой ветви с сопротивлением   (рис. 5.5).

е´

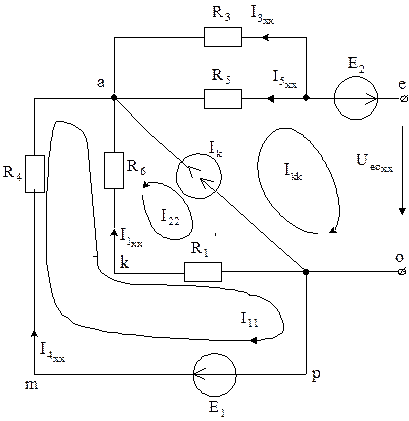
Рис. 5.5

По второму закону Кирхгофа для контура  aeoka, имеем:

,

     токи: 

получаем:   .

Ток найдем, используя метод контурных токов (см. рис. 5.5). Примем  и составим уравнение по методу контурных токов для контурного ток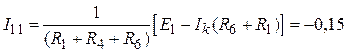а :

,

А.

Искомый ток

 А.

Соответственно

4.3. Для расчета   относительно зажимов ое , источники ЭДС  =  закорачиваем (==0), а источник тока   размыкаем , тем самым превращаем активный двухполюсник в, соответствующий ему, пассивный двухполюсник (см. рис. 5.6).

Таким образом,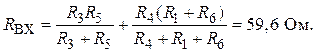 

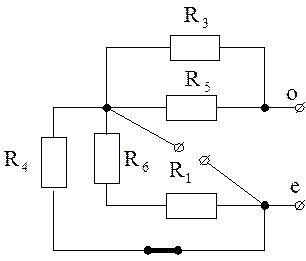
Рис. 5.6

4.4. Определяем ток :

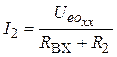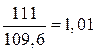= А.

5. Составление уравнения

энергетического баланса

(баланса мощностей)

При составлении уравнения баланса мощностей необходимо учитывать, что в тех ветвях цепи, где направление тока совпадает с направлением ЭДС, соответствующий источник ЭДС следует рассматривать как  генератор энергии, а в тех ветвях, где направления ЭДС и тока противоположны, источник ЭДС следует рассматривать как потребитель энергии, и в уравнение баланса он входит со знаком минус . Все сопротивления, независимо от направления протекающего через них тока, являются потребителями энергии.

Уравнение баланса мощностей для рассматриваемой схемы рис. 5.2 имеет вид

,

где  – напряжение на зажимах источника тока  .

Знак составляющей  мощности источника тока определяется следующим образом: знак «плюс» берется, если    и знак «минус», если .

Мощность источника тока равна:

.

Напряжение  определим, по второму закону Кирхгофа, задавшись положительным направлением обхода контура, включающего ветвь с источником тока, например, для контура   ):

.

Откуда

= В.

Окончательно, выражение для уравнения баланса мощностей с учетом найденного   запишется в виде

После подстановки числовых значений имеем 91,21=91,1 Вт.  

6. Построение потенциальной диаграммы

6.1. Для построения потенциальной диаграммы возьмем внешний контур  (рис. 5.2). 

Принимаем потенциал произвольной точки равным нулю ().

6.2. Производим расчет потенциалов остальных точек согласно выбранному направлению обхода контура (по часовой стрелке). Расчетные значения токов принимаем в соответствии с п. 1.4 задачи:

,

 В,

 В,

 В,

 В,

.

6.3. Определяем масштабы для напряжений    и сопротивлений   .

6.4. Построение диаграммы.  На диаграмме по оси абсцисс откладываем значения сопротивлений участков в последовательности расположения их в контуре; по оси ординат – потенциалы соответствующих точек (рис. 5.7).

Потенциальная диаграмма внешнего контура цепи:

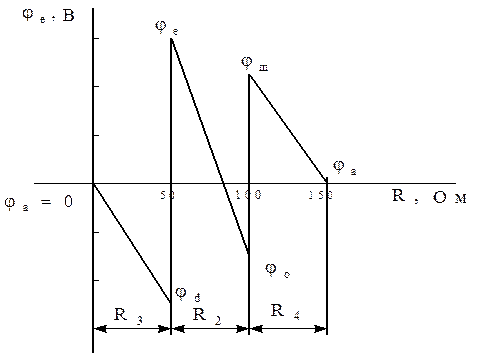
Рис. 5.7

Задача 2

Е2

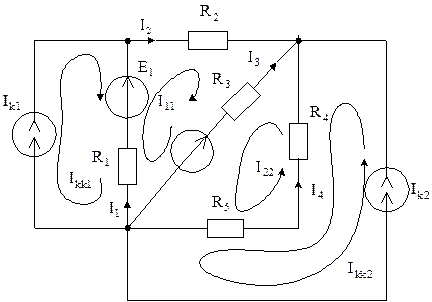
Рис. 5.8

Дано: ,,,,,….

Для цепи (рис. 5.8) в общем виде записать уравнения и формулы для определения токов по методу контурных токов.

1.  Количество независимых контуров  (количество уравнений)

=,

,    . 

2.  Система уравнений по методу контурных токов  (для контурных токов    и  ):

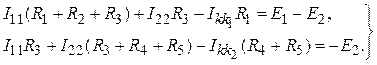
3.  Решение системы  дает значения  токов  и , что позволяет определить  действительные токи  по формулам:

, ,  ,  .

Задача 3

I2

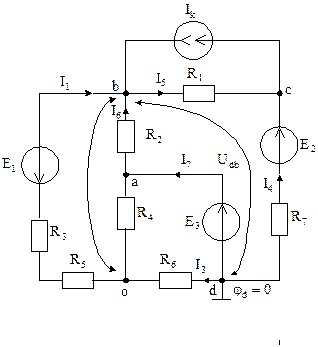
Рис. 5.9

Дано: , , , ,.

Для цепи (рис. 5.9) составить уравнения для расчета токов по методу узловых потенциалов. Определить напряжение  между узлами   и   . 

Особенностью расчета приведенной схемы является наличие ветви с источником ЭДС   , содержащей нулевое сопротивление.  В этом случае необходимо потенциал одного из узлов данной ветви принять равным нулю, например, потенциал узла d, , тогда потенциал узла  а равен .