КОНИЧЕСКИЕ ПРЕДАЧИ
Конические зубчатые колёса служат для передачи движения между валами, оси которых пересекаются под углом 10° < S < 180°. Обычно угол между осями S = 90° (рис. 1); конические передачи в этом случае называются ортогональными.
Вместо делительных цилиндров цилиндрических зубчатых передач при анализе движения и геометрических параметров конических передач используются делительные конусы. На рис. .1 образующие делительных конусов показаны штрих–пунктирными линиями. (Обычно начальные и делительные конуса совпадают). Углы между осями начальных конусов и их образующими обозначаются символами d1 и d2.
В случае цилиндрического колёса делительная окружность образуется пересечением делительного цилиндра плоскостью, ортогональной его оси. Аналогично делительную окружность конического колеса получают пересечением делительного конуса другим, дополнительным делительным конусом (ДДК). Оси делительного и ДДК совпадают, а их образующие взаимно перпендикулярны. Этим условиям соответствует множество ДДК, но обычно используют внешний, внутренний и средний ДДК.
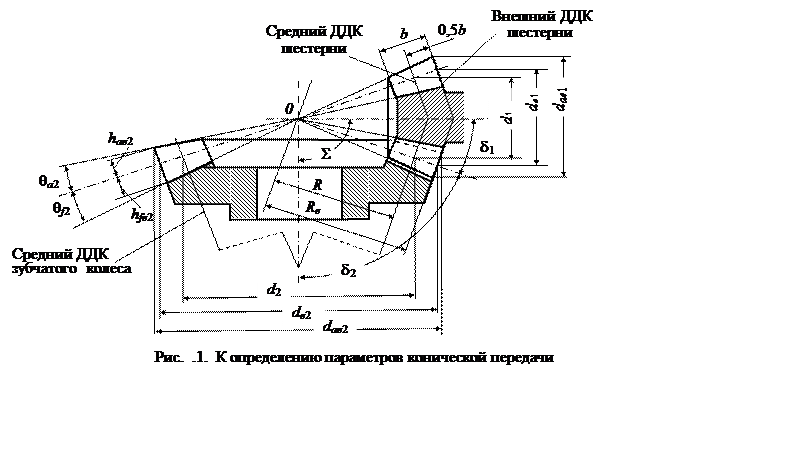
Сечение конического зубчатого колеса ДДК называют торцовым сечением; внешнему, внутреннему и среднему ДДК соответствуют внешнее, внутреннее и среднее торцовые сечения. Ширина зубчатого венца b равна расстоянию между внешним и внутренним торцовыми сечениями, измеренному по образующей делительного конуса.
Контроль размеров по внешнему конусу удобнее, эти размеры конических колёс указывают на чертежах. Размеры в среднем торцовом сечении используют при расчётах по контактным и изгибным напряжениям. Поэтому из множества возможных делительных окружностей конических колёс используют обычно внешнюю и среднюю делительные окружности. Размеры, относящиеся к внешнему торцовому сечению, помечают индексом е, например de1, de2, Re. Размеры, относящиеся к среднему торцовому сечению, помечают индексом т или записывают без индекса, например dт1, dт2, Rт или d1, d2, R. Символами R и Re обозначают соответственно среднее и внешнее делительные конусные расстояния. Между параметрами в среднем и внешнем торцовых сечениях имеют место следующие соотношения: Re = R+ 0,5b; de = d×Re/R. Модуль в торцовом внешнем сечении тte = тt Re/R.
Конические передачи могут быть прямозубыми (рис. .2а), косозубыми (или тангенциальными) (рис. .2б) и с дуговыми зубьями (рис .2в). Линии зубьев дуговых зубьев могут быть частью окружности, эвольвенты и других кривых линий. Для прямозубых передач торцовое и нормальное сечение совпадают, в этом случае модуль тte обычно принимают равным стандартному значению т.
 |
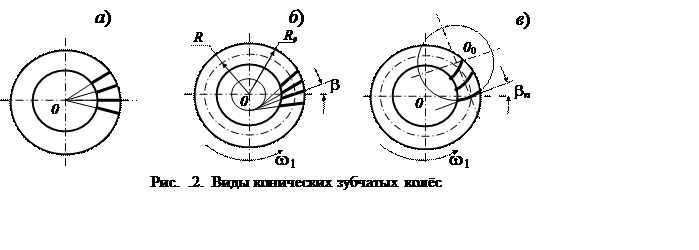С целью снижения концентрации напряжений по торцам зубьев и уменьшения возможности заедания прямозубых колёс используют зубья бочкообразной формы со съёмом металла начиная от среднего ДДК до 20 … 40 мкм на внешнем и внутреннем ДДК. Передачи с дуговыми зубьями наименее чувствительны к изменению взаимного положения шестерни и колеса, имеют наибольшую нагрузочную способность и плавность работы. Наибольшее распространение среди передач с дуговыми зубьями получили передачи с круговыми зубьями. Конические передачи с тангенциальными зубьями используются значительно реже по сравнению с дуговыми зубьями из-за низкой технологичности.
Передаточное отношение конических передач так же, как и в случае цилиндрических колёс, равно u = z2/ z1= d2/ d1. При S = 90° делительные диаметры конических колёс d1 = 2Rsind1 и d2 =2Rsind2 . Соответственно, передаточное число u = sind2 / sind1, или u = sind2 / cosd2 = tgd2.
.2. ОБРАЗОВАНИЕ ЗУБЬЕВ КОНИЧЕСКИХ ЗУБЧАТЫХ КОЛЁС
В процессе образования зубьев цилиндрических колёс делительный
цилиндр перекатывается без скольжения по начальной плоскости производящей
рейки, при этом движение резания параллельно начальной плоскости рейки. В случае
конических колёс имеет место качение делительного конуса конического колеса по
начальной поверхности производящего колеса диаметром 2Re. Производящее колесо и заготовка конического нарезаемого
колеса вращаются вокруг неподвижных осей (рис. .3).
(Если начальной поверхностью производящего колеса является плоскость, то такое производящее колесо называется плоским. Если начальной поверхностью производящего колеса является конус с углом при вершине 180°– 2qf , то такое производящее колесо называется плосковершинным).
Угол между направлениями зубьев на делительном конусе определяют по числу зубьев плоского производящего колеса (эквивалентного производящей рейки), которое равно zc = 2Re/mte. Для ортогональной конической передачи при S = 90° (рис. 1) диаметр плоского производящего колеса равен 2Re = (d2e1 + d2e2)1/2. Так как de1 = mtez1, de2 = mtez2, 2Re = mtezс то
zс = (z21 + z22)1/2,
где zс – обычно дробное число.
Соответственно, угол между направлениями зубьев равен 360°/zс.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
