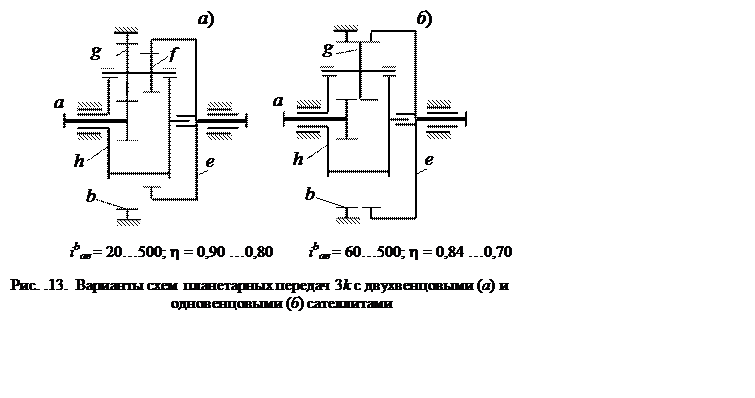
Ещё большие значения передаточных отношений имеют планетарные передачи, выполненные по схеме 3k (рис. .13).
Для передачи 3kпередаточное отношение ibaе = (wa – wb)/(we – wb). Умножив числитель и знаменатель на (wh – wb), получим
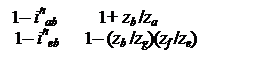 |
|||
|
|
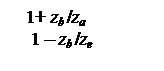 |
Для передачи с одновенцовыми сателлитами ibaе = ¾¾¾ .
Заметим, что разность чисел зубьев | zb – za |> 0 при равенстве диаметров dw-b = mzbи dw-e= m(ze+ x), где x– смещение при нарезании зубьев колеса е, т.е. zb – ze= x. Из условия симметричного расположения сателлитов (zb + za)/ nw = С1 и (zе + za)/ nw = С2 , где С1 и С2 – целые числа. Минимальная разность С1 – С2 = 1, т.е. (zb + za)/ nw – (zе + za)/ nw =1. Следовательно, zb– za = = nw и при числе сателлитов nw = 3 смещение x= 3.
 |
Звенья, которые вращаются вокруг основной оси и непосредственно воспринимают внешние нагрузки, называются основными. Предположим, что все звенья (солнечное колесо, водило и эпицикл) являются основными. Из условия равновесия при установившемся движении (без учёта потерь на трение) имеет место равенство нулю суммы трёх вращающих моментов
ТA + ТB + ТH = 0,
где ТA, ТB и ТH – соответственно, моменты на солнечном колесе, эпицикле и водило с учётом их направления (по или против часовой стрелки).
Из закона сохранения энергии в механической системе (без учёта потерь на трение) следует, что сумма всех мощностей также равна нулю:
ТA wA + ТB wВ + ТH wН = 0,
где wA , wВ и wН – соответственно, угловые скорости относительно неподвижной системы координат;
произведения Тiw i в данном равенстве принимаются с учётом знака.
Из данных равенств получим: ТH = – (ТA + ТB),
ТA wA + ТB wВ – (ТA + ТB) wН = 0,
– ТA /ТB = (wA – wН) / (wВ – wН) = 1/ iНАВ.
Аналогично, запишем: – ТA /ТН = 1/ iВАН и – ТВ /ТН = 1/ iАВН .
Для передачи на рис. .12, а при неподвижном водиле (wН = 0) получим
– Та /Тb = 1/ ihab = 1/(– zb/ za), или Та /Т b = za / zb. Таким образом, направления вращения колёс а и b противоположны, а направления моментов Та и Тb совпадают. Соответственно, Таwа = – Тbwb (рис. .14, а).
Для передачи на рис. .12, б при неподвижном колесе b (wВ = 0) получим
– Та /Тh = 1/ ibah = 1/(1 + zb/ za). Таким образом, направления моментов Та и Тh противоположны при совпадении направлений вращения колёс а и водило h (рис. .14, б).
Для передачи на рис. .12, в при неподвижном колесе а (wА = 0) получим
– Тb /Тh = 1/ iabh = 1/(1 + za/ zb). Направления моментов Тb и Тh противоположны при совпадении направлений вращения колёс bи водило h. (рис. .14, в).
Зная момент на выходном валу, можно определить момент на входном валу и соответствующими им тангенциальные силы с учётом числа сателлитов. Силы, действующие на опоры сателлитов (т. Оw на рис. . 12, а и .14, а) или в зацеплениях с неподвижными зубчатыми колёсами (т. C на рис. .14, б и т. D на рис. .14, в), определяются исходя из условий равновесия.
Обозначим Та момент, передаваемый от солнечного колеса одному сателлиту. При неподвижном водиле (рис. .14, а) тангенциальная сила Fta = Та/rа, а тангенциальная сила – Ftg=Fta. Из условия равновесия сателлита следует, что он нагружен парой сил Ftg. Соответственно, на колесо b действует сила Ftb= Ftg = Ftа. Момент на колесе b равен Тb = Ftаrb = –Та rb /rа и отношение моментов Та / Тb = – rа /rb = – zа /z b= – 1/ ihab.
При неподвижном колесе b (рис. .14, б) сила, действующая со стороны оси сателлита на водило, равна Fh = Тh/(rа+ rg), где Тh – момент, передаваемый от водила одному сателлиту. Из условия равновесия сателлита следует, что он находится под действием пары сил Ftg= 0,5Fg (в т.С – мгновенном центре вращения сателлита – сила Ftg от взаимодействия с неподвижным колесом b, а в т. А – от взаимодействия с солнечным колесом). Очевидно, что тангенциальная сила Fta = Ftg = 0,5Fh = 0,5Тh/(rа+ rg), Соответственно, момент Та = – Ftа rа и отношение Та /Тh = – 0,5rа/(rа + rg). Так как rg = 0,5(rb – rа), получим Та /Тh = – zа /(zа + z b) = –1/(1 + z b/zа) = –1/ ibah
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.