Геометрические параметры конических передач. Общая характеристика планетарных передач. Кинематика волновых передач, страница 3

       F_а  = F¢_r sin d₁ ± F¢_а  cos d₁ = F_t (tga sin d₁± sinb cos d₁) / cosb.

Знак + принимается, если направление вращения ведущего зубчатого колеса и направление винтовой линии зуба совпадают (рис. .2, б и в).

При расчётах на прочность конических колёс с непрямыми зубьями в качестве эквивалентных принимаются цилиндрические прямозубые колёса, диаметр которых d_v1 = d₁ /(cosd₁ cos²b) и d_v2 = d₂ /(cosd₂ cos²b), а эквивалентное число зубьев z_v1 = z₁ /(cosd₁ cos³b) и z_v2 = z₂ /(cosd₂ cos³b).

 . 3. 3. Контактная прочность прямозубой конической передачи

Условие контактной прочности зубьев записывают в виде

                             s_Н = Ö0,418 (qE_пр/r_пр) £ [s_Н] ,

где r_пр определяется по диаметрам эквивалентных колёс:

 

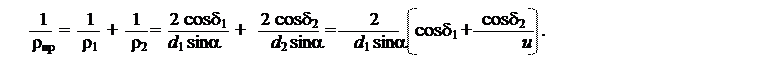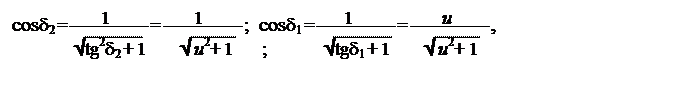Принимая во внимание тригонометрические равенства при S = 90°

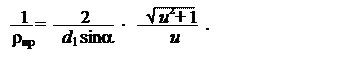получим

При определении удельной нагрузки qпринимается, что жёсткость (или податливость) зубьев постоянна по ширине колеса и, следовательно, нагрузка распределена также пропорционально расстоянию от вершины начального конуса и равна

                                          q= K_H (F_t /cosa) / b.

Заметим, что значения приведенного радиуса кривизны в различных сечениях зуба конического колеса пропорциональны диаметрам этих же сечений и, соответственно, расстоянию от вершины начального конуса. Таким образом, отношение q/r_пр также постоянно по длине зуба. Подставив полученные соотношения в формулу s_Н = Ö0,418 (qE_пр/r_пр), получим формулу расчётного контактного напряжения для конической передачи, аналогичную формуле для цилиндрической передачи, и соответствующее условие контактной прочности в виде

 

                                            

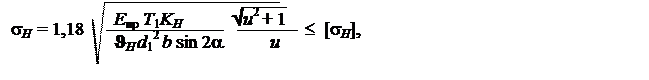где J_Н – коэффициент снижения нагрузочной способности конической передачи по сравнению с цилиндрической; J_Н  = 0,85.

При проектировочном расчёте полученную формулу преобразуют так, чтобы в результате расчёта были получены основные габаритные размеры конической передачи d_e  и R_e:

 

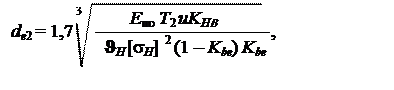где T₂ – момент на ведомом валу;

       K_be = b/R_e  – коэффициент ширины зубчатого венца относительно внешнего конического расстояния R_e; рекомендуемое значение K_be £ 0,3. В случае наиболее распространённого значения K_be= 0,285

 

                                d_e2 = 2,9    E_пр T₂ uK_Нb/  [s_Н] ² .

. 3. 3. Изгибная прочность прямозубой конической передачи

Условие изгибной прочности зубьев записывается в виде s_F £ [s_F], где расчётное значение напряжения определяется по формуле, аналогичной формуле для цилиндрических зубчатых колёс

                           s_F  = Y_FS F_t K_F / (J_F b m),

где J_F – коэффициент снижения нагрузочной способности конической передачи по сравнению с цилиндрической при изгибе; J_F  = 0,85;

      Y_FS  – коэффициент формы зуба определяется как для цилиндрических колёс, но при эквивалентном числе зубьев z_v = z /cosd. Обычно в виду повышенной опасности разрушения зубья конической шестерни нарезают с положительным смещением, а зубья конического колеса – с отрицательным смещением х₂  = – х₁.

. 3. 4. Коэффициенты расчётной нагрузки K_Н и K_F

Значения  K_Н и K_F при расчёте конических передач определяют аналогично цилиндрическим передачам. При равной степени точности изготовления значения динамических нагрузок конической передачи выше. Поэтому коэффициенты K_Нv и K_Fv определяют по тем же таблицам, но значения этих коэффициентов для конических колёс принимают на одну степень точности ниже цилиндрических.

Коэффициенты  K_Нb определяют в зависимости от значений  K_be и u, схемы передачи (консольная установка колеса и шестерни (рис. 6, а) или установка колеса и шестерни на двух опорах (рис. 6, б)) и в зависимости от вида опор. При консольной установке колёс K_Нb передач на роликовых опорах существенно меньше, чем при установке на шариковых опорах.

 

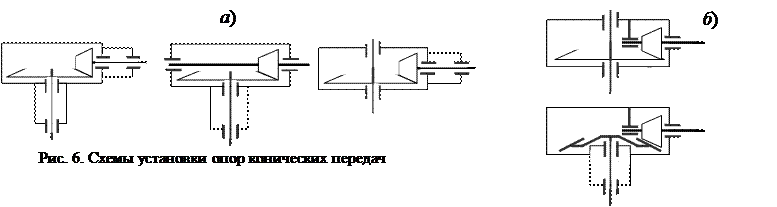
Коэффициент K_Fb = 1 + 1,5(K_Нb – 1) учитывает, что приработка оказывает более  благоприятное влияние  на контактную прочность, а также учитывает более тяжёлые последствия поломки зубьев по сравнению с усталостным выкрашиванием.

. 3. 5. Особенности расчёта передач с непрямыми зубьями